Use as seguintes etapas para mostrar que a sequência t n = 1 + 1 2 + 1 3 + … + 1 n - ln ⁡ n tem um limite. (O valor do limite é denotado por γ e é chamado constante de Euler.)(a) Desenhe uma figura como a Figura 6 com f x = 1 x e interprete t n como uma área [ou use 5 ] para mostrar que t n0 para todo n .(b) Interprete t n - t n + 1 = ln ⁡ n + 1 - ln �� n - 1 n + 1 �� como uma diferença de áreas para mostrar que t n - t n + 10 . Portanto t n é uma sequência decrescente.(c) Use o Teorema da Sequência Monótona para mostrar que t n é convergente.

Enunciado

(a) Galera, vamos fazer o seguinte desenho:

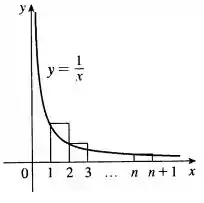
Aqui podemos ver que:

(b) Agora olha essa figura:

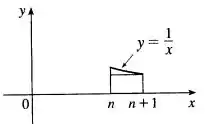
Ou seja, podemos escrever:

Portanto é uma sequência decrescente.

Portanto, é uma sequência decrescente e limitada, o que nos faz concluir, pelo Teorema da Sequência Monótona, que converge.

Ei, a resposta está no passo a passo :)