Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.11 - Ex. 10
Use a série binomial para expandir a função como uma série de Maclaurin e para encontrar os três primeiros polinômios de Taylor, , e . Plote a função e esses polinômios de Taylor no intervalo de convergência
Passo 1
Oii pessoal, tudo certo?
Essa questão pede algumas coisas, então vamos dividir em três momentos:
Primeiro, vamos achar a série de Maclaurin dessa função, comparando com a função da série binomial:
Pra fazer isso, a gente vai expandir os termos binomiais que acharmos pra generalizar os coeficientes de na série.
Segundo, vamos encontrar o intervalo de convergência da série, usando o teste da razão (ou da raiz).
Por último, vamos plotar a função e os polinômios , e , nesse intervalo de convergência.
Então vamos por a mão na massa!
Passo 2
Se a gente reescrever a função do enunciado como:
Vemos que basta substituir os valores e no lugar de colocar :
Agora, precisamos expandir esse termo binomial e descobrir o padrão.
Passo 3
Vamos começar a expandir o termo binomial:
Vamos encontrar esses padrões. Para :
- Os termos com par são negativos, e com ímpar são negativos, ou seja, temos um termo de
- Os numeradores são produtos dos números a partir de , somando de em , ou seja,
Portanto, o padrão para é:
Para :
Sendo assim, a nossa série é
E esta é a nossa série!
Passo 4
Vamos usar o teste da razão para calcular o intervalo de convergência:
Então,
Pelo teste da razão, a série converge para
Essa é o intervalo de convergência da série!
Passo 5
Como o intervalo de convergência é , vamos obter os plots em torno deste intervalo.
Os polinômios são:
Utilizando softwares para nos auxiliar, temos:
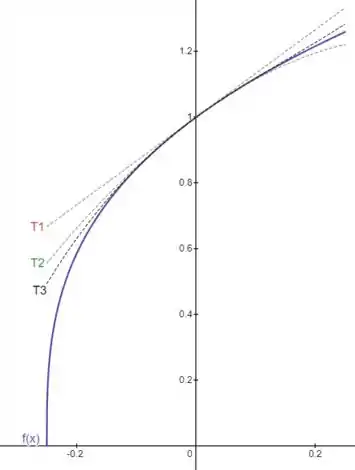
Resposta
