Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 40

Use uma série de Maclaurin na Tabela 1 para obter a série de Maclaurin da função dada.

f x = x 4 + x 2

Passo 1

Vamos lá pessoal, nessa questão temos que eonctrar a série Maclaurin da função:

f x = x 4 + x 2

Mas veja que devemos utilizar alguma das seguintes séries (séries que estão na tabela 1)

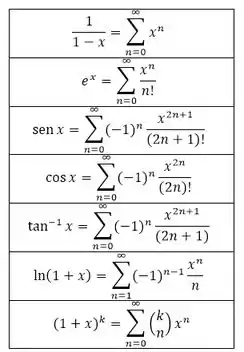
Devemos ver qual dessas funções mais se parece com a nossa função e fazer as manipulações matemáticas adequadas para chegar até a série de Maclaurin.

Passo 2

Perceba que inicialmente nenhuma das funções parece a nossa função:

f x = x 4 + x 2

Mas e se escrevermos ela de uma outra forma?

f x = x 4 + x 2 = x 4 + x 2 - 1 / 2

Podemos trabalhar um pouquinho mais com ela colocando 4 em evidencia e tirando da raiz

x 2 1 + x 2 4 - 1 / 2

Vamos olhar novamente as funções da tabela?

Passo 3

Veja que temos:

x 2 1 + x 2 4 - 1 / 2

Que é muito parecido com

1 + x k

Só precisamos considerar que o termo x 2 multiplicará a série após ela estiver pronta, considerar x 2 4 = y . E k =   - 1 2 . Assim co messa mudança de variáveis vamos ter:

x 2 . 1 + y k = x 2 ∑ n = 0 ∞ k n y n

Substituindo o que está em parênteses por sua série binomial com y substituído por x 2 / 4 e k = - 1 / 2

= x 2 ∑ n = 0 ∞ - 1 / 2 n x 2 4 n = x 2 ∑ n = 0 ∞ - 1 / 2 n x 2 n 2 2 n

Colocando x / 2 para dentro da série, aumentando os respectivos expoentes

= ∑ n = 0 ∞ - 1 / 2 n x 2 n + 1 2 2 n + 1

Resposta

f x = ∑ n = 0 ∞ - 1 / 2 n x 2 n + 1 2 2 n + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a série de Maclaurin para f ( x ) usando a definição da série de Maclaurin. [Assuma que f possui uma expansão em série de potências. Não mostre que R n x → 0 . ] Encontre também o raio de con
Use a definição da série de Taylor para encontrar os quatro primeiros termos não nulos da série para f ( x ) centrada no valor dado de a . f x = x 3 , a = 8
Use a definição da série de Taylor para encontrar os quatro primeiros termos não nulos da série para f ( x ) centrada no valor dado de a .
Encontre a série de Maclaurin para f ( x ) usando a definição da série de Maclaurin. [Assuma que f possui uma expansão em série de potências. Não mostre que R n x → 0 . ] Encontre também o raio de con
Encontre a série de Taylor para f ( x ) usando o valor dado a . [Assuma que f possui uma expansão em série de potências. Não mostre que R n x → 0 . ] Encontre também o raio de convergência associado.2