Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 7
Use a definição da série de Taylor para encontrar os quatro primeiros termos não nulos da série para centrada no valor dado de .
Passo 1
Fala turminha, tudo bem com vocês? Bora gabaritar essa juntos!?
Vamos entender o enunciado da questão. Bom, precisamos utilizar a definição da série de Taylor e encontrar os quatros primeiros termos não nulos da série da função que está centrada em .
Como resolver então? Vamos pensar juntos. Primeiro vamos relembrar a definição da série de Taylor
Repare que já temos a função e o deslocamento , que o enunciado no forneceu.
Agora basta expandirmos a serie até e aplicar , pois a questão quer os quatro primeiros termos.
Bora fazer isso!
Passo 2
Vamos relembrar a função e o deslocamento
Com o auxílio da equação 6 apresentada acima, temos que a série de Taylor será dada por:
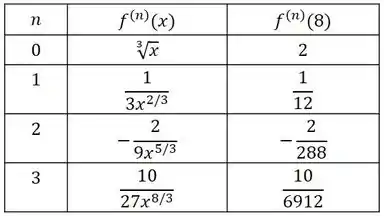
Agora, vamos representar em uma tabela os quatro primeiros termos e os respectivos valores:
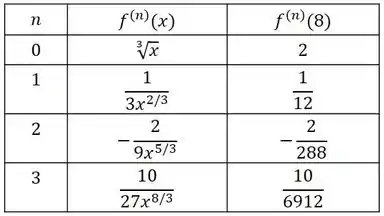
Resposta
