Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.3 - Ex. 25

(a) Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial. Imprima-o e esboce algumas curvas solução sem resolver a equação diferencial.

(b) Resolva a equação diferencial.

(c) Use o SCA para desenhar vários membros da família de soluções obtida na parte (b). Compare com as curvas da parte (a).

Passo 1

(a) Bom, pessoal. Vamos desenhar o campo de direções da equação diferencial:

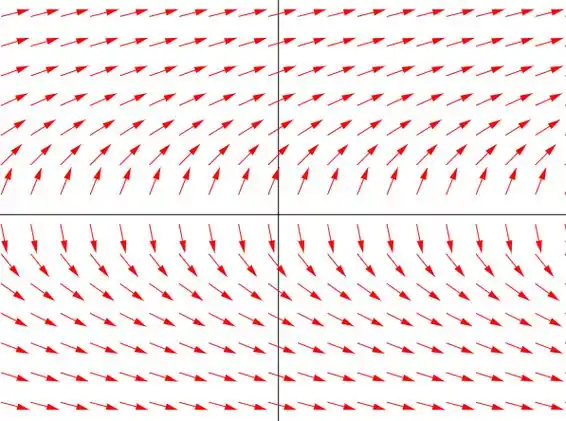
Passo 2

(b) Agora vamos resolver a equação, pessoal. Ela é do tipo separável, então basta rearranjar cada lado e integrar:

Passo 3

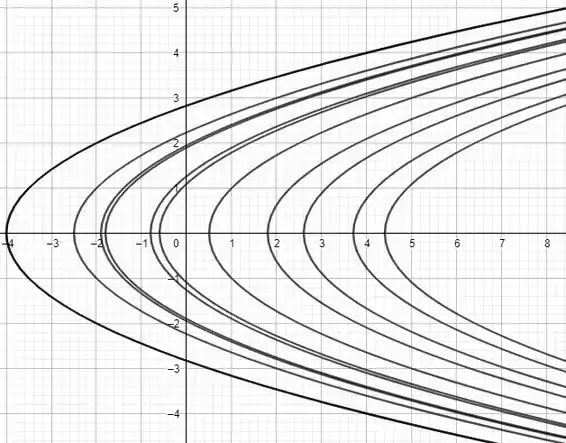
Comparando os desenhos do item (a) e (c), a gente percebe que o campo de direções realmente parece estar seguindo uma trajetória de parábola, como deveria ser.

Resposta

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera com raio de 1m está a uma temperatura de 15° C . Ela está dentro de uma esfera concêntrica com raio de 2m e temperatura de 25° C . A temperatura T r a uma distância r do centro comum das du

Um tanque contém 1000L de água salgada com 15k g de sal dissolvido. Água pura entra no tanque a uma taxa de 10L / m i n . A solução é mantida bem misturada e escoa do tanque na mesma taxa. Quanto sal

Em contraste com a situação do Exercício 36 , as experiências mostram que a reação H 2 + B r 2 → 2 H B r satisfaz a lei de troca d H B r d t = k H 2 B r 2 1 2 e, portanto, para essa reação a equação d

Quando uma gota de chuva cai, ela aumenta de tamanho; assim, sua massa em um instante t , é uma função de t,m t . A taxa do aumento da massa é k m t para alguma constante positiva k . Quando aplicamos

O ar em uma sala com volume 180m 3 contém 0,15% de dióxido de carbono inicialmente. Ar mais fresco com apenas 0,05% de dióxido de carbono entra na sala a uma taxa de 2m 3 / m i n e o ar misturado sai