Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 23
Determine o volume do sólido dado.
Limitado pelos planos , , e
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!
Para resolver essa questão, precisamos identificar e desenhar a região de integração no plano delimitada pelos planos dados. Depois vamos montar a integral dupla para calcular o volume do sólido e assim resolver a integral dupla.
Primeiro, vamos identificar e desenhar a região no espaço tridimensional delimitada pelos panos , , e .
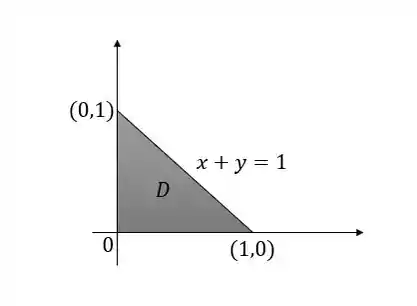
A projeção desse sólido no plano forma um triângulo com vértices em e .
Passo 2
Para calcular o volume do tetraedro, podemos montar uma integral dupla. Observando os limites dos planos, podemos escrever a integral de volume na forma iterada. A equação do plano é .
Os limites de integração são:
- varia de 0 a 1.
- varia de 0 a .
A integral de volume é dada por:
Passo 3
Primeiro, integramos em relação a :
Substituindo os limites de integração em :
Agora, integramos essa expressão em relação a :
Integrando termo a termo:
Substituindo os limites de integração em :