Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.1 - Ex. 2
Se , use a soma de Riemann com , para estimar o valor de . Tome os pontos amostrais como os cantos inferiores esquerdos dos sub-retângulos.
Passo 1
O exercício quer que estimemos o valor da integral sobre um retângulo usando uma soma de Riemman. Com isso, escrevemos
Com isso, nós substituímos a integral por uma soma. O enunciado pediu para dividirmos o intervalo no eixo em partes e o intervalo no eixo em partes. Com isso, obtemos
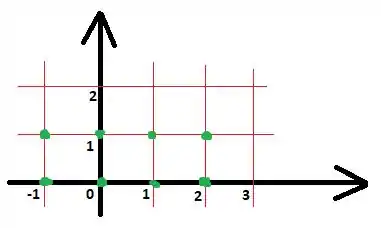
Também foi pedido para considerar como pontos amostrais os cantos inferiores esquerdos dos retângulos, como indicado pelos pontos verdes na figura. Esses pontos são
Passo 2
Devemos calcular o valor da função em cada um desses pontos usando que :
Como todos os são iguais, podemos escrever a soma como
Como , substituindo os valores das funções:
Com isso, a estimativa da integral é