Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 52

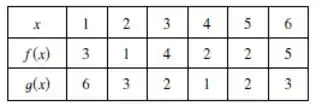
Use a tabela para determinar o valor de cada expressão.

  1. f g 1 (b) g f 1 (c) f f 1

(d) g g 1 (e) g   o   f ( 3 ) (f) ( f   o   g ) ( 6 )

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente determinar o valor de algumas composições de funções em pontos determinados, usando a tabela:

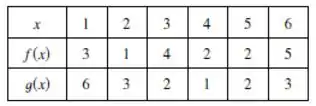
Pra isso, vamos olhar primeiro o valor que tá dentro dos parênteses, que será o nosso x , e localizar ele na tabela. Daí, se a questão nos pede a função composta f g x , que é o mesmo que f   o   g , localizando o x , teremos o g ( x ) .

Então, com o valor de g ( x ) , obtido da tabela, encontramos o valor de f naquele ponto, na linha de f ( x ) . O processo é o mesmo para a composição g f x = g   o   f e f ( f x = f   o   f e g g x = g   o   g , beleza?

Vamos lá!

Passo 2

Pra resolver o item (a), queremos primeiro encontrar f g 1 . Isso significa que temos que encontrar f ( g x ) no ponto x = 1 .

Olhando na tabela, vamos achar g ( 1 ) , olhando a coluna onde x = 1 e a linha de g ( x ) :

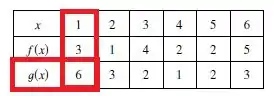
Repare que a interseção da linha com a coluna nos fornece:

g 1 = 6

Agora, como a gente quer achar a composição f ( g 1 ) e g 1 = 6 , temos que encontrar o valor de f ( 6 ) . Olhando novamente na tabela,

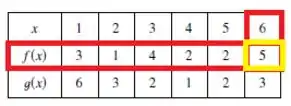
Nós encontramos:

f 6 = 5

Logo,

f g 1 = 5

Passo 3

Agora vamos resolver o item (b) e encontrar g f 1 . Isso significa que vamos encontrar g ( f x ) , quando x = 1 , da mesma forma que fizemos no passo anterior.

Então, vamos começar achando f ( 1 ) na tabela:

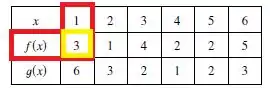
Então, de acordo com a tabela,

f 1 = 3

Assim, precisamos encontrar g ( 3 ) . Olhando novamente na tabela, temos:

g f 1 = g 3

g f 1 = 2

Passo 4

Vamos seguir o mesmo raciocínio para resolver a letra (c), encontrando f f 1 .

Então, vamos achar f ( 1 ) na tabela:

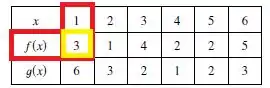
Da mesma forma que no passo anterior, temos:

f 1 = 3

Só que agora queremos f ( f 1 ) que é igual a f ( 3 ) . Então, temos:

f f 1 = f ( 3 )

f f 1 = 4

Passo 5

Vamos seguir o mesmo processo para acharmos (d) g g 1 , encontrando g ( 1 ) .

De acordo com a tabela, temos:

g 1 = 6

Então, localizando g ( 6 ) na tabela, vamos ter:

g ( 6 ) = 3

Logo,

g g 1 = 3

Passo 6

Para acharmos (e) g   o   f 3 , temos que lembrar que g   o f = g ( f x ) . Então, vamos encontrar f ( 3 ) .

De acordo com a tabela, temos:

f 3 = 4

Então, localizando g ( 4 ) na tabela, vamos ter:

g ( 4 ) = 1

g f 3 = 1

Passo 7

Por último, para achar (f) f o   g 6 = f g 6 , vamos começar encontrando g ( 6 ) .

De acordo com a tabela, temos:

g 6 = 3

Então, localizando f ( 3 ) , teremos:

f ( 3 ) = 4

f g 6 = 4

Valeu, galera! Até a próxima! 😉

Resposta

  1. g 1 = 5 (b) g f 1 = 2 (c) f f 1 = 4

(d) g g 1 = 3 (e) g   o   f 3 = 1 (f) ( f   o   g ) 6 = 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam f ( x ) = x e g ( x ) = 1 - x .Escreva as fórmulas para f ∘ g e g ∘ f Determine o domínio de cada umaDetermine a imagem de cada uma
Sejam f ( x ) = 2 - x e g ( x ) = x + 1 3 . Determine f ∘ g ( - 1 ) g ∘ f ( 2 ) f ∘ f ( x ) g ∘ g ( x )
Sejam f ( x ) = 2 - x 2 e g ( x ) = x + 2 .Escreva as fórmulas para f ∘ g e g ∘ f Determine o domínio de cada umaDetermine a imagem de cada uma
Sejam f ( x ) = 1 x e g ( x ) = 1 x + 2 . Determine f ∘ g ( - 1 ) g ∘ f ( 2 ) f ∘ f ( x ) g ∘ g ( x )
Determine (a) o domínio e (b) a imagem de y = { - x - 2 , se - 2 ≤ x ≤ - 1 , x , se - 1x ≤ 1 e - x + 2 , se 1x ≤ 2 .