Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 46b
Use uma tabela de valores de para estimar o limite com 4 casas decimais.
Passo 1
Olá, meu amigo. Yuri aqui estarei te ajudando a continuar a resolução desta atividade.
Na letra a) utilizamos um gráfico para estimar o valor do limite da função dada, agora o que iremos fazer é utilizarmos uma tabela.
Para resolver este item da questão, construiremos uma tabela de valores, onde será confrontado com , e a partir dai iremos observar para qual valor a função se caminha no seu limite ao infinito.
Passo 2
Temos então:
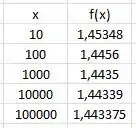
Por meio da análise da tabela podemos observar que quanto maior o valor de , se aproxima de . Logo,
Resposta
Exercícios de Livros Relacionados
Calculef . underset(x - + oo)(lim) ((5 x^3 - 6 x + 1)/(6 x^2 + x + 3))
Calculee ) underset(x - + oo)(lim) ((5 x^3 - 6 x + 1)/(6 x^3 + 2))
Prove que underset(x - oo)(lim) root(n)(x) = + oo , onde n0 é um natural.
Calculea ) underset(x - + oo)(lim) (sqrt(x) + 1)/(x + 3)
Calculeg ) underset(x - + oo)(lim) ((5 x^3 + 7 x - 3)/(x^4 - 2 x + 3))