Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.2 - Ex. 2
Prove que , onde é um natural.
Passo 1
Galera, a primeira coisa que a gente tem que notar é que a função “raiz” é contínua, e por isso, é só a gente substituir o valor de e ver o que dá!
Para ilustrar melhor, dá uma olhada no gráfico de algumas funções “raiz”:
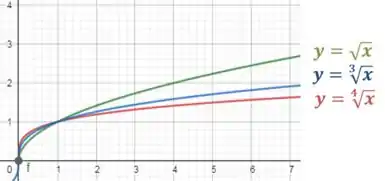
Substituindo por infinito, a resposta vem de imediato. Apesar de esquisito, é só isso mesmo!
É só repara que conforme aumenta, também aumenta.
Resposta
Exercícios de Livros Relacionados
Calcule o limite, se existir.underset(t - 0)(lim) (1)/(t sqrt(1 + t)) - (1)/(t)
Calcule o limite. lim x → 3 - x x - 3
Calcule o limite. lim y → - ∞ 3 - y 5 + 4 y 2
Calcule o limite, se existir. lim x → - 1 x 2 - 4 x x 2 - 3 x - 4
Calcule o limite, se existir.30. lim x → - 4 x 2 + 9 - 5 x + 4