Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.4 - Ex. 15

Use o Teorema 5.4.2 para calcular as somas e verifique suas respostas usando um recurso computacional.

∑ k = 1 30 k ( k - 2 ) ( k + 2 )

Passo 1

Vamos fazer umas mudancinhas aí:

∑ k = 1 30 k k - 2 k + 2 = ∑ k = 1 30 k ( k 2 - 4 ) =   ∑ k = 1 30 k 3 - 4 k

Agora a gente separa em duas:

∑ k = 1 30 k 3 -   ∑ k = 1 30 4 k

Vamos tirar a constante pra fora:

∑ k = 1 30 k 3 - 4 ∑ k = 1 30 k

Agora tá do jeito que a gente aplica o teorema.

Passo 2

O teorema nos fala que:

∑ k = 1 n k = n n + 1 2

E

∑ k = 1 n k 3 = n n + 1 2 2

Então bora fazer isso na nossa!

∑ k = 1 30 k = 30 30 + 1 2 = 930 2 = 465

∑ k = 1 30 k 3 = 30 30 + 1 2 2 = 465 2 = 216225  

Passo 3

E agora, juntando os dois e usando a constante:

∑ k = 1 30 k 3 - 4 ∑ k = 1 30 k

= 216225 - 4 465

= 214365

Show! Calculamos o somatório!

Vamos verificar na calculadora do site S y m b o l a b :

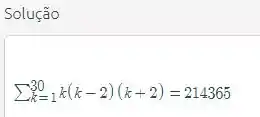
Certinho!

Resposta

2 14365

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 14, ache o limite e, quando aplicável, indique os teoremas de limite usados. 5 )lim z → - 2 ⁡ z ³ + 8 ³
Nos exercícios de 1 a 14, ache o limite e, quando aplicável, indique os teoremas de limite usados. 4 )lim x → 3 ⁡ 2 x ² - 4 x + 5 ²
Para a função g x representada graficamente aqui, determine os seguintes limites ou explique por que eles não existem a ) lim t → - 2 ⁡ f ( t ) b ) lim t → - 1 ⁡ f ( t ) c ) lim t → 0 ⁡ f ( t ) d ) li
Quais das afirmações a seguir com relação à função y = f ( x ) representada graficamente aqui são verdadeiras? E quais são falsas? a ) lim x → 0 ⁡ f ( x ) existe b ) lim x → 0 ⁡ f ( x ) = 0 c ) lim x
Quais das afirmações a seguir com relação à função y = f ( x ) representada graficamente aqui são verdadeiras? E quais são falsas? a ) lim x → 2 ⁡ f ( x ) não existe b ) lim x → 2 ⁡ f ( x ) = 2 c ) li