Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.9 - Ex. 16
Use o Teorema da Divergência para calcular a integral de superfície , ou seja, calcule o fluxo de através de .
é a superfície do sólido limitado pelos hemisférios e pelo plano
Passo 1
E aiii minha turma, tudo na paz!?
Nessa questão devemos resolver a seguinte integral de superfície, utilizando o teorema do divergente:
Onde, temos:
E, é a superfície do sólido limitado pelos hemisférios e pelo plano .
A primeira coisa, é lembrar do teorema do divergente:
Esse teorema permite transformar a integral de superfície em uma integral tripla de volume.
Onde o é:
Sendo,
Observe que devemos pegar cada componente de e derivar em relação a .
Feito isso, devemos olhar para a região . Uma dica é você plotar essas curvas dadas, como ele falou que é um hemisfério, vamos ter duas esferas e um plano em . Desse jeito:
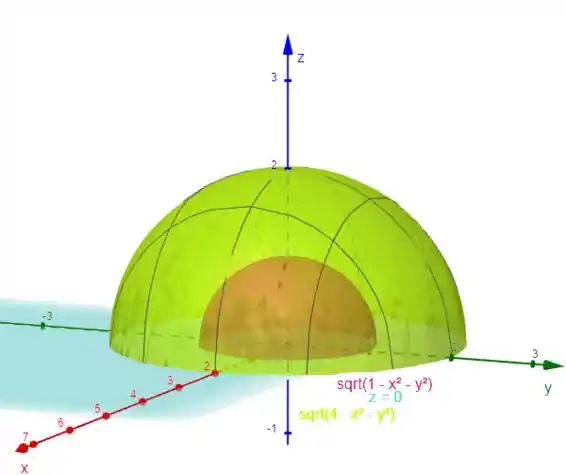
Nossa região de interesse está entre a esfera vermelha e a esfera verde, e acima do plano azul .
Como se trata de coordenadas esféricas, podemos usar as relações:
Onde,
Repare que o ângulo vai até graus, isso acontece por causa do plano .
Agora não tem erro, é só aplicar na integra!
Vamos nessa!
Passo 2
Repare na integral, precisamos achar o divergente de :
Já vimos que é:
Onde temos:
Logo, o divergente é escrito como:
Fazendo as derivadas em relação a . Temos que o divergente da função é:
Logo a integral que devemos resolver é:
Passo 3
Agora precisamos especificar o tipo de região que estamos trabalhando pra poder fazer a integral de forma correta.
Já vimos que a região de interesse está dentro duas esferas, entre uma de raio igual a e outra de raio igual a , e acima do plano . Assim:
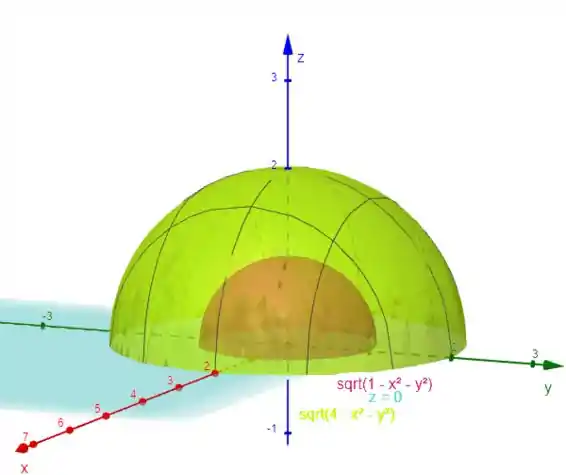
Logo se trabalharmos com coordenadas esféricas teremos:
Onde,
Pois não deixa ir para o plano inferior. Por isso esse ângulo varia até .
Logo, substituindo na integral vamos ter:
Lembrando que um elemento infinitesimal de volume em coordenadas esféricas é expresso como:
Assim, temos a seguinte integral:
Olhe pra os integrando, colocamos nessa ordem de integração:
Mas nesse caso tanto faz a ordem, pois todos os integrandos estão variando em termos de números.
Passo 4
Agora vamos simplificar um pouco a integral.
Utilizando a relação trigonométrica:
Vamos ficar com:
Fazendo a primeira integral em temos:
Aplicando os limites de integração, ficamos com:
Integrando em primeiro vamos ter:
Aplicando os limites de integração, temos:
Isso foi possível, porque repare que nenhum dos termos dentro da integral depende de . Ai podemos utilizar desse bizu.
Agora nos restou uma integral em . Mas antes vamos separar as integrais, assim:
Passo 5
Para resolver a primeira integral, é utilizado uma técnica de integração por partes.
Mas esse tipo de integral já é bastante conhecido, e temos o seu valor tabelado da seguinte forma:
Logo, substituindo o valor acima na integral e integrando a segunda integral, vamos ter:
Aplicando os limites de integração:
Assim, o valor da integral de superfície aplicando o teorema do divergente é: