Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 2b

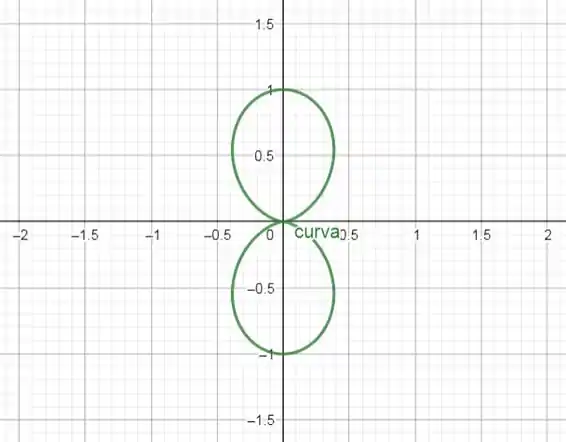
Passe a curva dada para coordenadas polares e desenhe-a:

( x 2 + y 2 ) 3 2 = y ²

Passo 1

Primeiramente, sabemos que:

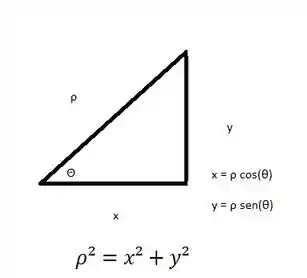
Logo, substituindo:

( x 2 + y 2 ) 3 2   = ρ 2 3/2 e ρ ² s e n 2 θ =   y ²

ρ 2 3/2 = ρ ²   s e n ² ( θ )

Simplificando:

ρ =   s e n ² ( θ ) -> em coordenadas polares

Passo 2

Para desenharmos a curva, basta fazermos uma tabela de pontos e ligar estes uns aos outros.

Passo 3

Ligando-se os pontos, teremos:

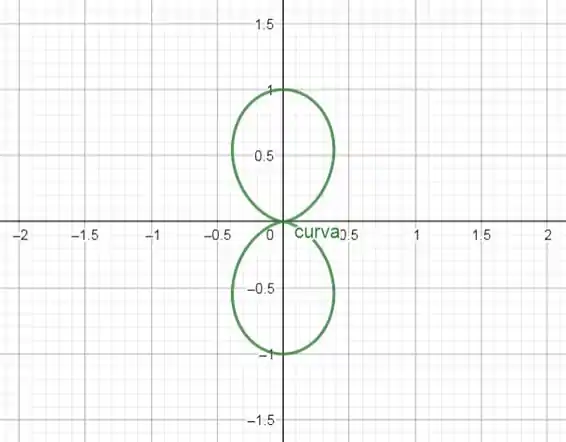
Resposta

ρ =   s e n ² ( θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a curva com a equação x 2 3 + y 2 3 = 1 e usa a simetria para achar seu comprimento.
Trace a curva e estime visualmente seu comprimento. A seguir, encontre seu comprimento exato. y = x + cos ⁡ x ,0 ≤ x ≤ π 2
Encontre o comprimento de arco da curva do ponto P ao ponto Q. x ² = y - 4 3P 1 ,5 Q ( 8 ,8 ) ²
Desenhe a curva y = x 4 - x 3 ,0 ≤ x ≤ 4 . Calcule os comprimentos das poligonais inscritas com n = 1 ,2 e 4 lados. (Divida o intervalo em subintervalos iguais.) Ilustre esboçando essas poligonais (co
Repita o Exercício 27 para a curva y = x + sen x , 0 = x = 2 pi