Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.8 - Ex. 5

Use o teorema de Stokes para calcular .

, �� formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices , com orientação para fora. (Sugestão: use a equação .)

Passo 1

Oi galera, tudo bem?

Nessa questão precisamos calcular uma integral de superfície de um rotacional, usando o teorema de Stokes. Ela sugere usarmos a equação , que é essa:

Onde e são duas superfícies com como fronteira.

Nossa superfície é:

é formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices , com orientação para fora.

Vamos considerar as superfícies e é o fundo que não é considerado do cubo.

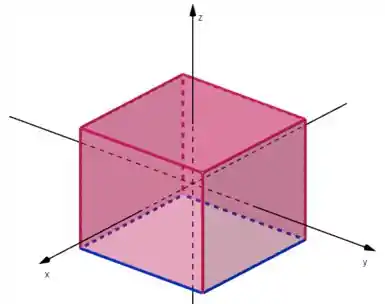
A curva é esse quadrado azul, e a superfície é a superfície desse quadrado (em rosa mais claro). Tanto quanto estão na altura .

O que vamos fazer é calcular a integral:

Pra isso, começamos pelo , depois parametrizar e fazer:

Passo 2

Bom, vamos começar calculando o rotacional de :

Como nosso campo é

Então:

Passo 3

Primeiro a coordenada do rotacional:

Derivando em função de , com constantes:

Então:

Passo 4

A segunda coordenada:

Derivando em função de , com constantes:

Daí:

Passo 5

E a última coordenada do rotacional:

Derivando em função de , com constantes:

E aí:

Então o rotacional fica:

Passo 6

Agora precisamos parametrizar essa superfície .

Como ela é parte do plano :

E como é um quadrado, com as coordenadas indo de até :

Passo 7

Pra calcular , vamos fazer as derivadas de :

E então:

Passo 8

Tá quase acabando...

Agora vamos aplicar a nossa parametrização

No rotacional

Então:

E a integral fica:

Vamos resolver isso!

Passo 9

Fazendo o produto escalar, que é simplesmente multiplicar coordenada a coordenada e somar:

Só que esse é o quadrado :

Integrando primeiro em função de , com constante:

Aplicando os limites de integração:

Integrando em função de :

Ou seja:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema de Stokes para calcular ∬_S vec grad xx vec F * d vec S . vec F (x , y , z) = e^(x y) + e^(x z) hat j + x^2 z hat k S é m e t a d e d o e l i p s o i d e 4 x^2 + y^2 + 4 z^2 = 4 , é o r

Use o Teorema de Stokes para calcular ∮ C F → ⋅ d r → . Em cada caso, C é orientado no sentido anti-horário quando visto de cima. F → x , y , z = i ^ + x + y z j ^ + x y - z k ^ , C é o limite da part

Use o Teorema de Stokes para calcular ∫ C F .d r . Em cada caso, C é orientado no sentido anti-horário visto de cima.10- F x , y , z = x i + y j + x 2 + y 2 k , C é a fronteira da parte do paraboloide

Use o Teorema de Stokes para calcular ∫ ∫ S r o tF .d S 2- F x , y , z = y zi + x zj + x yk S é a parte do paraboloide z = 9 - x 2 - y 2 que está acima do plano z = 5 , com orientação para cima.

Use o Teorema de Stokes para calcular ∫ ∫ S r o tF .d S 3- F x , y , z = x 2 e y z i + y 2 e x z j + z 2 e x y k , S é o hemisfério x 2 + y 2 + z 2 = 4 ,z ≥ 0 , com orientação para cima.