Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.8 - Ex. 11

  1. Use o Teorema de Stokes para calcular ∫ C F → ⋅ d r → ,   onde

    2. F → x , y , z = x 2 z i → + x y 2 j → + z 2 k →

    e C é a curva da intersecção do plano x + y + z = 1 com o cilindro x 2 + y 2 = 9 com orientação no sentido anti-horário quando visto de cima.

  2. Trace o gráfico do plano e do cilindro com domínios escolhidos de forma a ver a curva C e a superfície que você usou na parte ( a ) .
  3. Determine as equações paramétricas para C e use-as para traçar o gráfico de C .

Passo 1

Oi, galera! Tudo bem?

A questão tem 3 partes: a parte a) pede para usarmos o Teorema de Stokes para calcular a integral de linha:

∫ C F → ⋅ d r →

Onde o campo vetorial é:

F → x , y , z = x 2 z i → + x y 2 j → + z 2 k →

e C é a curva da intersecção do plano

x + y + z = 1

com o cilindro

x 2 + y 2 = 9

O Teorema de Stokes traz que:

∫ C F ⋅ d r = ∬ S r o t F ⋅ d S

Onde:

d S = n   d A

Ou seja, podemos calcular a integral dupla do rotacional de F para obter o valor da nossa integral de linha. Aqui, n é nosso vetor perpendicular à superfície. Então nossa integral será:

∬ S r o t F ⋅ d S = ∬ S r o t F ⋅ n   d A

Então, vamos precisar calcular o rotacional de F , achar o valor do vetor n e fazer o produto escalar entre eles. Daí, teremos uma integral dupla, que basta resolvermos para chegarmos no valor da integral de linha que o exercício pediu.

Depois, pede para traçarmos o gráfico do plano e do cilindro para visualizarmos a curva C da parte a). Daí vamos pra parte c), onde vamos precisar parametrizar essa curva e traçar o gráfico de C usando essas equações paramétricas.

Bora lá!

Passo 2

  1. Vamos começar achando o vetor normal da nossa superfície: curva de fronteira está no plano

    z = 1 - x - y

    Ou:

    x + y + z - 1 = 0

    Se temos um plano com equação:

    A x + B y + C z + D = 0

    O vetor normal a esse plano é dado por:

    n → = 〈 A , B , C 〉

    Aqui, comparando com nosso plano:

    x + y + z - 1 = 0

    Temos:

    A = 1 B = 1

    C = 1

    Então nosso vetor será:

    n → = 〈 1,1 , 1 〉

    Pronto! Temos nosso vetor normal.

    Passo 3

    Legal! O próximo passo é determinar o rotacional de F → :

    r o t F = ∇ × F → = i →   j →   k →   ∂ ∂ x   ∂ ∂ y   ∂ ∂ z   x 2 z   x y 2   z 2  

    Fazendo o produto vetorial dessa matriz:

    = i → ∂ ∂ y ( z 2 ) - ∂ ∂ z ( x y ² ) + j → ∂ ∂ z ( x ² z ) - ∂ ∂ x ( z ² ) + k → ∂ ∂ x ( x y ² ) - ∂ ∂ y ( x ² z )

    Fazendo as derivadas parciais, ficamos com:

    r o t F = ∇ × F → = 〈 0 , x 2 , y 2 〉

    O produto vetorial entre ∇ × F → e n → fica:

    ∇ × F → ⋅ n → = 0 , x 2 , y 2 ⋅ 1,1 , 1 = x 2 + y 2

    Passo 4

    Substituindo na nossa integral:

    ∬ S r o t F ⋅ n   d A

    Ficamos com:

    ∬ S x 2 + y 2   d A

    Legal! O próximo passo é determinar a região de integração. No plano x y , temos:

    x 2 + y 2 = 9

    A projeção no plano x y é um círculo de raio 3 . Como temos uma circunferência completa, de raio 3 , centrada na origem, os limites de integração são:

    { 0 ≤ r ≤ 3   0 ≤ θ ≤ 2 π  

    E o elemento de área vai ser:

    d A = r d r d θ

    Também usamos a equação:

    x 2 + y 2 = r 2

    Então, nossa integral se torna:

    ∬ S x 2 + y 2   d A = ∫ 0 2 π ∫ 0 3 r 2   r   d r   d θ

    Passo 5

    Agora é calcularmos a integral:

    ∫ 0 2 π ∫ 0 3 r 2   r   d r   d θ

    Multiplicando os termos:

    ∫ 0 2 π ∫ 0 3 r 3 d r d θ

    Começando pela integral em r que é a integral de dentro:

    = ∫ 0 2 π r 4 4 0 3 d θ

    Aplicando os limites de integração:

    3 4 4 ∫ 0 2 π d θ =

    Finalizando a integral em θ e aplicando os limites de integração:

    ∫ C F → ⋅ d r → = 81 4 ⋅ 2 π = 81 π 2

    Passo 6

  2. Vamos para a parte b). Plotando o gráfico do cilindro

    3. x 2 + y 2 = 3

    e do plano

    x + y + z = 1

    Temos:

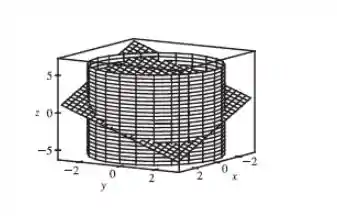
    A interseção entre o cilindro e o plano é justamente a curva C da nossa integral de linha:

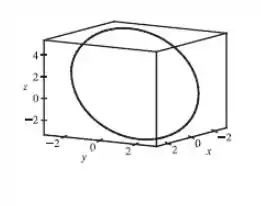
    Passo 7

  3. Fazemos agora a parametrização dessa curva C . Ela é dada pela interseção das curvas:

x 2 + y 2 = 3

e

x + y + z = 1

A parametrização do cilindro pode ser dada por coordenadas cilíndricas. Com r = 3 , temos:

x = 3 c o s c o s   t  

y = 3   s e n t

Com

0 ≤ t ≤ 2 π

Agora vamos encontrar o valor de z em termos de t . Substituindo x e y na equação do plano:

3 c o s c o s   t   + 3   s e n t + z = 1

Isolando, ficamos com:

z = 1 - 3 c o s t - 3 s e n t

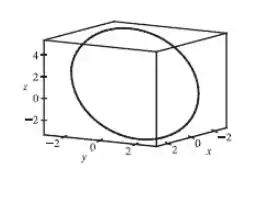
Então nossas equações paramétricas são:

r → t = { x = 3 c o s t   y = 3 s e n t   z = 1 - 3 c o s t - 3 s e n t  

Resposta

a ∬ S c u r l   F → ⋅ d S = 81 π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule: ∫ C 4 x y - 3 x 2 z 2 d x + 2 x 2 d y - 2 x 3 zd z Onde C é a interseção da superfície: x 2 3 + y 2 4 + z 2 = 1 Com z ≥ 0 , com o plano y = 1 . Indique a orientação escolhida.
Use o Teorema de Stokes para calcular ∬ S r o tF → ⋅ d S → . F → x , y , z = 2 y cos ⁡ zi → + e xs e n zj → + x e y k → S é o hemisfério x 2 + y 2 + z 2 = 9 ,z ≥ 0 , orientado para cima.
Como o teorema de Stokes generaliza o teorema de Green?
O que é o teorema de Stokes? Como se pode interpretá-lo?
Resuma os resultados do capítulo sobre campos conservativos.