Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.8 - Ex. 1
Dado um hemisfério e uma parte de um paraboloide, suponha que seja um campo vetorial sobre cujas componentes tenham derivadas parciais contínuas. Explique por que
Passo 1
Olá, tudo bem? Se você olhar o teorema do livro vai ver o seguinte:
Se e são suas superfícies orientadas com a mesma curva de fronteira .
Então precisamos ver se as nossas regiões possuem a mesma equação de fronteira.
Passo 2
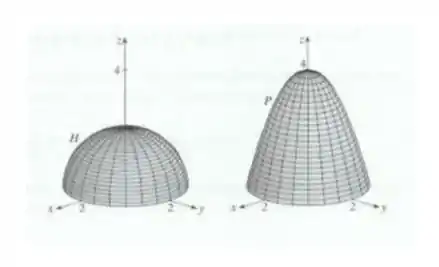
No nosso caso, essas duas regiões são o hemisfério e a parte do paraboloide , que no plano possuem a mesma equação de fronteira: , como podemos ver no desenho.
Show! Então essas duas regiões satisfazem a equação do passo :
Resposta
Exercícios de Livros Relacionados
Seja C a circunferência de raio a , no plano 2 x + 2 y + z = 4 , centrada no ponto 1 ; 2 ; - 2 . Se F x , y , z = y - x; z - x; x - y , determine o valor de a para que: ∮ C Fd r = - 8 3 π .
Calcule ∬ S r o t F →. n →d s Onde F x , y , z = x - x 2 z ; y z 3 - y 2 ; x 2 y - x z e S é qualquer superfície cuja borda seja uma curva fechada no plano x y .
Calcule ∬_S r o t (vec F) . vec n d s , onde F (x , y , z) = (2 x y ; 0 ; - x z) e S é a superfície do elipsóide:(x^2)/(4) + (y^2)/(9) + (z^2)/(16) = 1
Calcule int_C F d r , Onde:F (x , y , z) = (e^(- y) - z e^(- x) ; e^(- z) - x e^(- y) ; e^(- x) - y e^(- z)) E C é a curva parametrizada:sigma (t) = ((ln (1 + t))/(ln 2) ; sin ((pi t)/(2)) ; (1 - e^t)
Calcule:int_C (2 x y z + sin x) d x + (x^2 z + e^y) d y + (x^2 y + (1)/(z)) d z Onde C é a curva parametrizada por: sigma (t) = (cos^3 t ; sin^2 t ; (t + 1)^2) , 0 = t = pi .