Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 2a
Utilizando a ideia intuitiva de limite, calcule:
Passo 1
Fala galera! Vamos resolver essa questão! Temos que calcular o limite abaixo usando a ideia intuitiva de limite:
Beleza, mas qual a ideia intuitiva de limite?!
O limite é como ficar de olho no que acontece com uma função quando a variável se aproxima de um certo valor. É tipo observar para onde a função está indo à medida que a variável se aproxima desse ponto, mesmo que ela nunca realmente atinja esse ponto!
Pegando a nossa função , por exemplo. A medida que nos aproximamos de , ou seja com números como ou a função se aproxima de um certo número , então é nosso limite em !
Passo 2
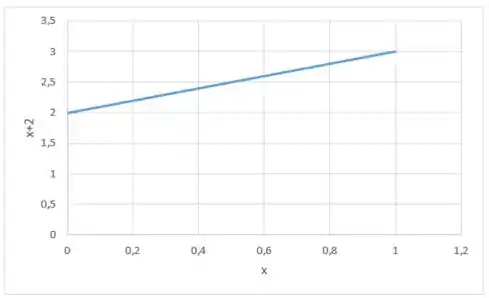
Para calcular o nosso limite usando essa ideia intuitiva vamos fazer um gráfico, primeiro pegando valores menores que :
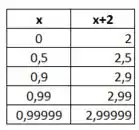
Desenhando temos:
Agora pegamos valores maiores que :
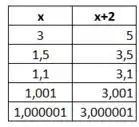
Desenhando:
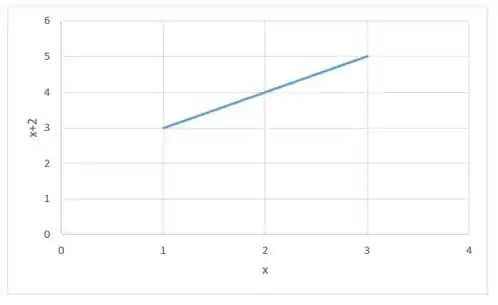
Podemos perceber que a medida que se aproxima ded , tanto pela direita quanto pela esquerda, então se aproxima ded , dessa forma podemos dizer que: