Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 33

Utilize uma calculadora gráfica ou um computador para estimar a coordenada x dos pontos de intersecção da curva y = x 4 e y = 3 x - x 2 . Se D é a região limitada por essas curvas, estime ∬ D x d A .

Passo 1

Oi pessoal, tudo bem?

Temos uma questão que fornece duas curvas em função de x que irão se interceptar em algum ponto criando uma região D . Iremos desenhar essas funções utilizando uma ferramanta gráfica qualquer e ficará bastante claro quais o ponto em que essas funções se interceptam.

Após isso é so integrar a função com os limites de integração encontrado.

Passo 2

O primeiro passo é esboçar as curvas para identificar os pontos de intersecção:

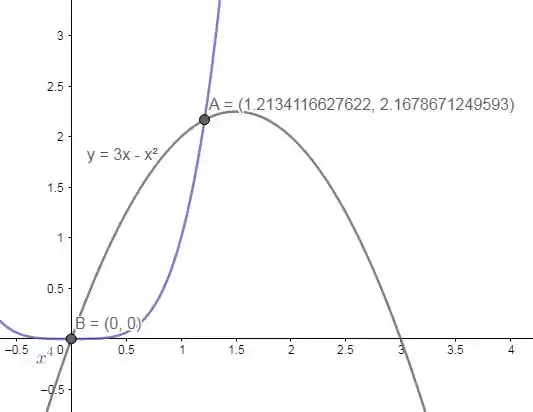
Veja que os pontos de intercepção são B = ( 0,0 ) e A = ( 1.213 ,   2.167 ) , veja também que a função y = x 4 é o limite inferior durante toda a região D e que y = 3 x - x 2 é função superior. Isso significa que os limites de integração em y são:

x 4 ≤ y ≤ 3 x - x 2

Enquanto que para x são:

0 ≤ x ≤ 1,213

Passo 3

Agora que achamos os limites, é só aplicar e resolver a integral. Temos que:

D = x , y | 0 ≤ x ≤ 1,213   , x 4 ≤ y ≤ 3 x - x 2  

Como os limites de integração de y são funções de x , então temos que integrar em y primeiro:

∬ D f x , y d A = ∫ 0 1,213 ∫ x 4 3 x - x 2 f ( x , y ) d y d x

Como f x , y = z , temos:

V = ∫ 0 1,213 ∫ x 4 3 x - x 2 x d y d x

Vamos resolver a integral de dentro:

∫ x 4 3 x - x 2 x d y = x y x 4 3 x - x 2

Agora, aplicando os limites de integração, temos:

∫ x 4 3 x - x 2 x d y = x 3 x - x 2 - x 4

∫ x 4 3 x - x 2 x d y = 3 x 2 - x 3 - x 5

Logo, substituindo, temos:

∫ 0 1,213 ∫ x 4 3 x - x 2 x d y d x = ∫ 0 1,213 3 x 2 - x 3 - x 5 d x

Passo 4

Agora é só resolver:

∫ 0 1,213 3 x 2 - x 3 - x 5 d x = 3 x 3 3 - x 4 4 - x 6 6 0 1,213

Agora, aplicando os limites de integração, temos:

∫ 0 1,213 3 x 2 - x 3 - x 5 d x = 3 1,213 3 3 - 1,213 4 4 - 1,213 6 6

Resolvendo, temos:

∫ 0 1,213 3 x 2 - x 3 - x 5 d x = 0,7126

Logo:

∬ D f x , y d A = 0,7126

Resposta

∬ D f x , y d A = 0,7126

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 2∫ x 2 4 f ( x , y ) d y d x
Determine o volume do sólido por subtração de dois volumes.O sólido no primeiro octante sob o plano z = x + y , acima da superfície z = x y e delimitada pela superfície x = 0 , y = 0 e x 2 + y 2 = 4 .
Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ 0 y f ( x , y ) d x d y
Use um sistema de computação algébrica para determinar o volume exato do sólido.Limitado por z = 1 - x 2 - y 2 e z = 0 .
Use um sistema de computação algébrica para determinar o volume exato do sólido.Abaixo da superfície z = x 3 y 4 + x y 2 e acima da região limitada pelas curvas y = x 3 - x e y = x 2 + x para x ≥ 0 .