Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 41
Use um sistema de computação algébrica para determinar o volume exato do sólido.
Abaixo da superfície e acima da região limitada pelas curvas e para .
Passo 1
E aí, meus queridos! Tudo na tranquilidade?
A questão pede para usarmos um software para calcular o volume do sólido limitado pelas regiões:
Abaixo da superfície e acima da região limitada pelas curvas e para .
O que vamos fazer aqui é montar a integral:
Definindo e os limites de integração da região . Daí jogamos num software, como o WolframAlpha, essa integral e ela nos retornará o valor exato do volume .
Bora pra resolução!
Passo 2
Vamos começar definindo para conseguirmos os limites de integração. Lembrando que a região se encontra no plano .
A região sob qual o sólido está acima é limitada por:
E
E essa região que o enunciado menciona é justamente , então vamos plotar essas duas curvas.
O domínio de integração no plano , para é:
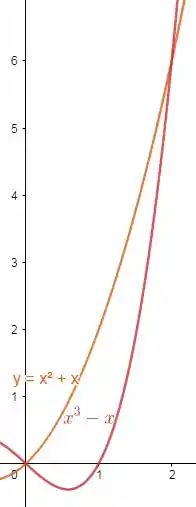
Olhando para o eixo , vemos que as intersecções das duas curvas estão em:
e
Como mostra a seta azul da imagem.
Já para os valores de , temos que o limite inferior é:
E o superior é:
A função é a que limita o sólido superiormente, o próprio enunciado já nos traz que essa superfície é dada por:
Assim, o volume é dado por:
Veja que colocamos como integral de dentro a integral , já que depende de em seus limites de integração.
Passo 3
Fazendo a integral exata usando uma calculadora gráfica (aqui, usei o como o WolframAlpha):
Temos: