Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 43
Use um sistema de computação algébrica para determinar o volume exato do sólido.
Limitado por e .
Passo 1
Oii, pessoal! Tudo joia?
A questão pede para usarmos um software para calcular o volume do sólido limitado pelas regiões:
e
O que vamos fazer aqui é montar a integral:
O que vamos precisar encontrar aqui é e os limites de integração da região .
Daí jogamos num software, como o WolframAlpha, essa integral e ela nos retornará o valor exato do volume .
Bora ver como fica nossa resolução!
Passo 2
Vamos começar encontrando nossos limites de integração, que saem da nossa região .
Como nossa região é no plano , achamos a interseção de
No plano fazendo
Obtemos
Assim o domínio de integração é a região interna a essa circunferência, cujo gráfico é:
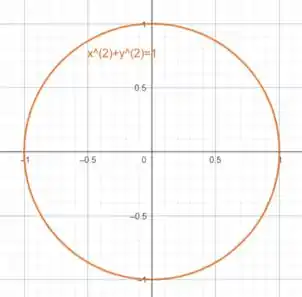
Aqui vamos escrever a região como uma região do Tipo I, onde está entre duas constantes e está entre duas funções.
Dessa forma, isolando :
Aplicando a raiz nos dois lados da equação:
Olhando o gráfico, dá pra ver que está entre -1 e 1.
Em coordenadas cartesianas essa região é descrita como:
Passo 3
Olhando nosso sólido:
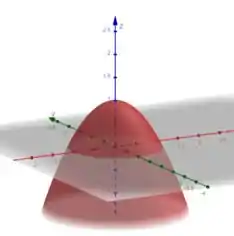
Ele será o volume de:
Acima do plano , que é onde delimita por baixo nosso sólido.
Assim, o volume é dado por:
Veja que colocamos como integral de dentro a integral , já que depende de em seus limites de integração.
Fazendo a integral exata usando uma calculadora gráfica, temos: