Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.1 - Ex. 15

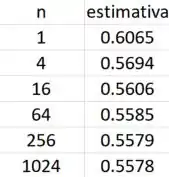
Utilize uma calculadora programável ou computador (ou comando-soma de um CAS) para estimar

∬ R e - x 2 - y 2 d A

Onde R = 0,1 × 0,1 .   Utilize a Regra do Ponto Médio com os seguintes números quadrados de tamanhos iguais: 1 ,   4 ,   16 ,   64 ,   256 e 1 0 24 .

Passo 1

Fala, galera. Tudo belezinha?

A questão quer que a gente calcule a integral dada pela Regra do Ponto Médio, utilizando algum programa top pra resolver, nos dando números quadrados de tamanhos iguais para nos ajudar.

A fórmula da Regra do Ponto Médio é essa aqui, ó:

∬ R f x , y d A   ≈ ∑ i = 1 m ∑ j = 1 n f x - i , y - j ∆ A

A região que iremos trabalhar vai de 0 ≤ x ≤ 1 no eixo das abscissas, e no eixo das ordenadas 0 ≤ y ≤ 1 . Um quadradão, beleza?

Com isso, os valores de quadrados perfeitos irão dividir a nossa região em subretângulos, e m e n nos diz a respeito da quantidade deles em cada eixo.

Respira, não pira!

Passo 2

Vamos fazer o Ponto Médio para o quadrado de tamanho 1 .

Com isso, teremos m = 1 e n = 1 . É como se fosse a distância do nosso retângulo tanto no eixo x quanto no eixo y .

Sabendo quem é nossa função, então:

∬ R e - x 2 - y 2 d A   ≈ ∑ i = 1 1 ∑ j = 1 1 f x - i , y - j ∆ A

Qual o ponto médio desse intervalo? 1 2 , para os dois eixos, ou seja, x - i , y - j .

E a área desses retângulos é ∆ A = 1 ⋅ 1 = 1

Podemos concluir que:

∬ R e - x 2 - y 2 d A = f x - i , y - j ∆ A

= f 1 2 , 1 2 ⋅ 1

Substituindo na função, temos:

e - 1 2 2 - 1 2 2

e - 1 4 - 1 4 ≈ 0.6065

Passo 3

Agora vamos tentar o quadrado de tamanho 4 .

Podemos representar assim:

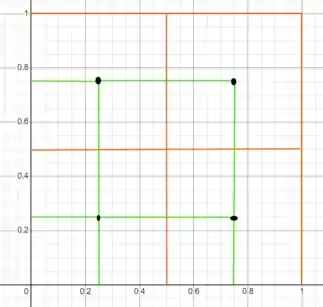
Dividimos a região 0,1 × 0,1 em 4 quadrados, definindo m = 2 e n = 2 .

E os pontos médios?

Estão marcados como pontinhos pretos no gráfico, mas serão assim:

x - 1 = y - 1 = 1 4

x - 2 = y - 2 = 3 4

A área de cada subretângulo será:

∆ A = 1 2 × 1 2 = 1 4

Colocando na nossa fórmula

∬ R e - x 2 - y 2 d A ≈ f x - 1 , y - 1 ∆ A + f x - 1 , y - 2 ∆ A + f x - 2 , y - 1 ∆ A + f x - 2 , y - 2 ∆ A

= ∆ A f 1 4 , 1 4 + f 1 4 , 3 4 + f 3 4 , 1 4 + f 3 4 + 3 4

Colocando esses valores na função teremos

= 0.5694

Jogando os quadrados que faltam ( 16 ,   64 ,   256   e   1024 ) no programa, teremos esses valores.

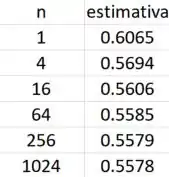
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.8. A figura mostra curvas de nível da função f no quadrado R = 0,1 × 0,1 . Use-as para estimar ∫ ∫ f ( x , y ) d A com precisão nas unidades.
15.6. Uma piscina de 20 por 30 pés é enchida com água. A profundidade da piscina é medida a cada intervalo de 5 pés, começando de um canto, e os valores foram anotados na tabela. Estime o volume de ág
O mapa de contornos mostra a temperatura, em graus Fahrenheit, às 3 horas da tarde do dia 1° de maio de 1996, no Estado do Colorado. (O Estado mede 388 mi de leste a oeste e 276 mi de norte a sul.) Ut
Determine ∫ 0 3 f ( x , y ) d x e ∫ 0 4 f ( x , y ) d y . f x , y = y x + 2
15.5. Calcule a integral iterada. ∫ 0 2 ∫ 0 π 2 x s e n ⁡ y d y d x