Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.1 - Ex. 10
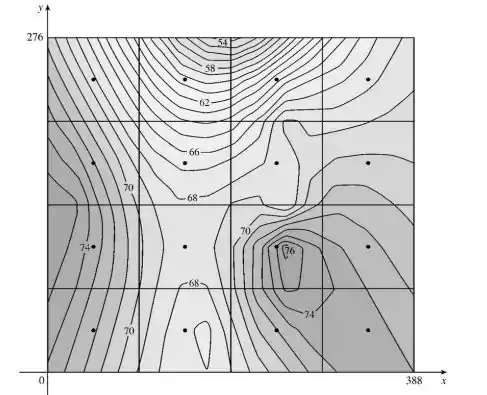
O mapa de contornos mostra a temperatura, em graus Fahrenheit, às 3 horas da tarde do dia 1° de maio de 1996, no Estado do Colorado. (O Estado mede 388 mi de leste a oeste e 276 mi de norte a sul.) Utilize a Regra do Ponto Médio com para estimar a temperatura média do Colorado nessa hora.
Passo 1
Fala, galerinha! Como vocês estão?
A questão traz um mapa de temperatura de certa região em certo horário e pede para que a gente ache a média de temperatura nesse instante mostrado no mapa.
O valor médio de uma função de duas variáveis em um certo retângulo é:
Onde é a área desse retângulo , que faz parte do domínio da função.
O que vamos precisar fazer é definir uma origem para nosso retângulo de análise e calcular essa área como a área de um retângulo.
Depois, vamos precisar encontrar o valor de:
E fazemos isso usando a Regra do Ponto médio para integrais duplas:
Onde são as coordenadas do ponto médio de cada sub-retângulo do retângulo total . é a função nesse ponto, ou seja, nesse caso será a temperatura no ponto, e é a área de cada sub-retângulo.
Como os valores das curvas no mapa representam a temperatura, podemos dizer que é igual ao valor da temperatura no ponto médio de cada sub-retângulo, que a gente encontra olhando os valores de temperaturas das curvas.
Essa soma
Os índices de são e e variam de 1 a e de 1 a , respectivamente. é o número de divisões em sub-retângulos na direção de e na direção de . Então a quantidade de sub- retângulos que vamos ter é .
No nosso caso o enunciado pede , então vamos ter que dividir em 16 sub-retângulos.
Ufa! Vamos aplicar todos esses conceitos.
Passo 2
Podemos iniciar calculando o valor da área de .
Vamos começar definindo uma origem para o retângulo , que corresponde a toda a imagem que o enunciado nos deu. Podemos colocar a origem no canto inferior esquerdo.
Então nosso terá as dimensões:
E:
Calculando a área de como calculamos a área de um retângulo qualquer (lado vezes lado).
Passo 3
Bem, a gente precisa usar o teorema do ponto médio aqui, para achar o valor da integral dupla:
O enunciado nos diz que , agora o trabalho que temos que fazer é subdividir a imagem, em 4 retângulos na direção de e 4 na direção de , ou seja, 16 retângulos.
Então , que é a área de um sub-retângulo, podemos achar calculando a área de 1 retângulo desse, onde um lado vai ser 388 dividido por 4 e o outro 276 dividido por 4, já que cada dimensão de foi dividida em 4 partes. Então, fica o seguinte
Onde mi são milhas, unidade de comprimento.
Passo 4
Já temos informações para usar o teorema do ponto médio:
Agora para obter os valores dos pontos médios de cada sub-retângulo.
Olhando para imagem, por exemplo, o ponto médio do primeiro sub-retângulo é , de acordo com a imagem, a temperatura nesse ponto é próxima de 72, já que o ponto está em uma linha entre a temperatura de 70 e 74 graus Fahrenheit.
Então, para os demais 16 sub-retângulos:
Encontrando o valor da função (temperatura) em cada um dos 16 pontos médios, olhando pelas curvas do mapa, vamos ter:
Resolvendo a soma dentro das chaves, temos:
Passo 5
Agora podemos determinar a temperatura :
Substituindo o valor da integral dupla da função temperatura que encontramos no passo 3:
Fazendo essa conta, teremos:
Então, no Colorado, no dia primeiro de maio de 1996, às três horas da tarde, estava uma temperatura de aproximadamente Fahrenheit