Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.1 - Ex. 6
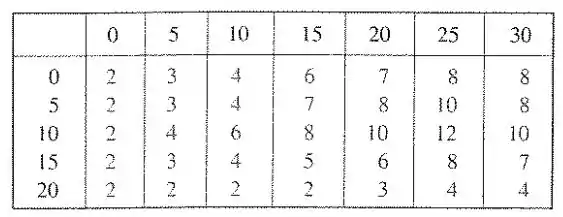
15.6. Uma piscina de 20 por 30 pés é enchida com água. A profundidade da piscina é medida a cada intervalo de 5 pés, começando de um canto, e os valores foram anotados na tabela. Estime o volume de água da piscina.
Passo 1
Nós precisamos estimar o volume da piscina. As informações que temos é que a piscina é retangular, e mede 20 por 30 pés. Vamos chamar a área da piscina de e imaginar que este retângulo está contido no plano . Então temos que
A gente pode interpretar também que a água seria o volume de um sólido acima desse retângulo. A gente pode descrever a forma desse volume como uma função de e , ou seja
Passo 2
Essas informações que a gente coletou, vão ajudar bastante agora, porque para estimar o volume da piscina nós podemos usar o teorema do ponto médio.
A gente pode esquematizar a piscina separando em 6 subretângulos
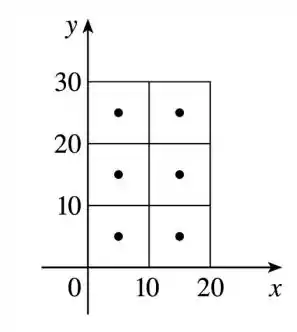
Repare que a área de cada subretângulo é de , então
Na componente de temos dois retângulos, e três retângulos em , então e . A gente não precisava necessariamente separar nessa quantidade de subretângulos, poderia ser mais ou menos, tudo depende da precisão que você busca.
Mas agora podemos usar o teorema do ponto médio
Agora para obter os valores dos pontos médios, a gente olha na tabela, por exemplo, o ponto médio do primeiro subretângulo é , na tabela isso corresponde a .