Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 77
Utilize um computador para estudar o comportamento da família de funções . Como a forma da função é afetada por uma mudança do valor de ?
Passo 1
Eaee, belezinha?? Bom... queremos utilizar um software matemático para plotar várias funções no seguinte formato:
Onde é uma constante.
Aqui a gente vai aplicar alguns valores de e ir plotando. Com isso, iremos analisar o que acontece quando alteramos o valor de , certinho??
Agora bora lá!! 😉
Passo 2
Traçando alguns gráficos para diferentes valores de :
Para
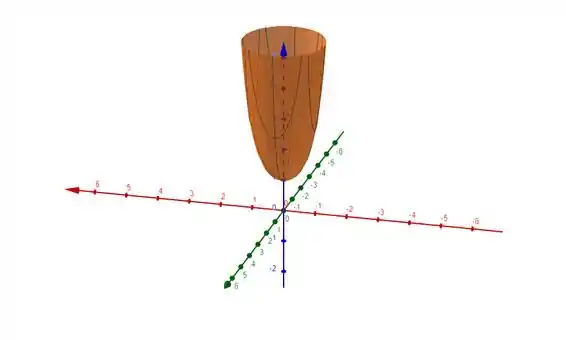
Para
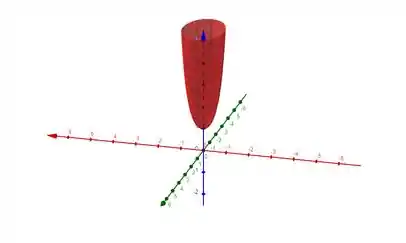
Para
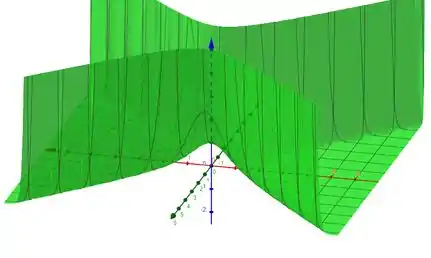
Para
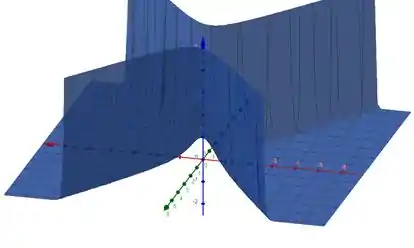
Passo 3
Com esses gráficos no mesmo espaço, obtemos:
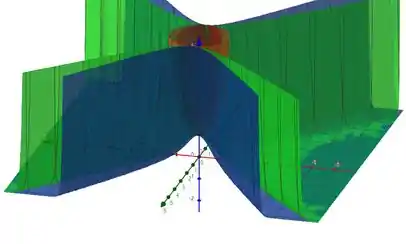
Podemos perceber que, independente do valor de , quando se trata do eixo é o mesmo para todos os gráficos, já que se o valor de não vai influenciar a função.
Agora para outros valores, temos que quanto maior o valor de a superfície tente a ser mais achatada próxima da origem, de forma que a figura se parece com um paraboloide.
E, quando é negativo, para certos valores de a função , mais precisamente quando , fazendo essa parte se “sobrepor” no limite.
Resposta
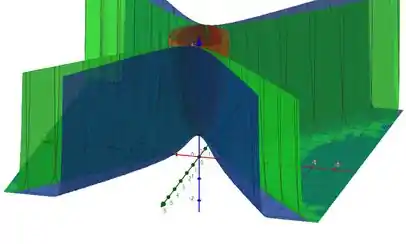
Para valores positivos de , temos uma figura parecida com um paraboloide.
E, quando é negativo, para certos valores de a função , mais precisamente quando , fazendo essa parte se “sobrepor” no limite.