Descreva as superfícies de nível da função.
Passo 1
Olá, meu querido. Vamos resolver essa atividade junto, beleza?
A gente tem a função:
E precisamos descrever as superfícies de nível.
Para descrever as superfícies de nível da função, basta fazer
As superfícies de nível de uma função são análogas às curvas de nível, mas em dimensões superiores. Para uma função de três variáveis uma superfície de nível é o conjunto de pontos que resultam em um valor constante da função.
As superfícies de nível são então como as curvas de nível. As curvas de nível estão em , enquanto as superfícies de nível em .
Então ao invés de termos uma representação bidimensional da nossa função, teremos o comportamento dessa função em 3 dimensões, para diferentes valores para .
Passo 2
Vamos então analisar o comportamento da nossa função:
Se ,
Então temos o gráfico para que possamos visualizar:
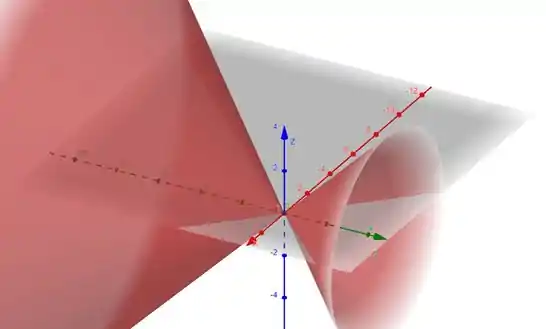
Ou seja, temos um cone com vértice na origem com eixo em .
Se ,
Podemos visualizar um exemplo onde :
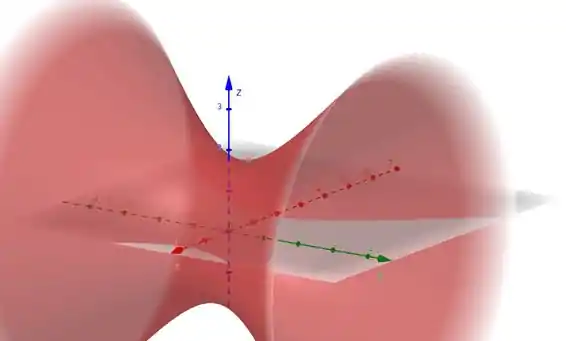
Ou seja, uma família de hiperboloides de uma folha com eixo em .
Se
Temos então uma visualização para :
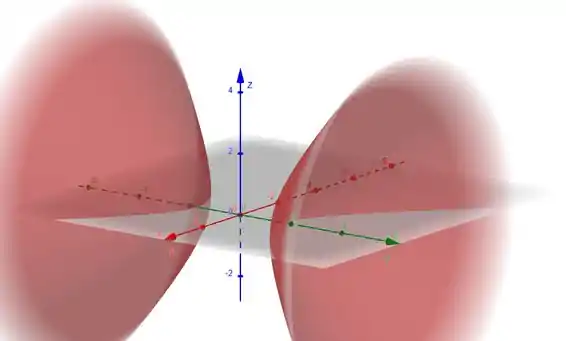
ou seja, uma família de hiperboloides de duas folhas com eixo em .
Resposta
Se , , ou seja, um cone com vértice na origem com eixo em .
Se , , ou seja, uma família de hiperboloides de uma folha com eixo em .
Se , , ou seja, uma família de hiperboloides de duas folhas com eixo em .