Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 51

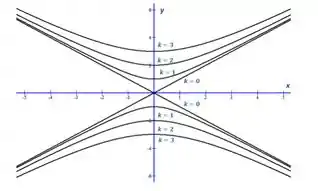
Faça o mapa de contorno da função mostrando várias curvas de nível.

f x , y = y 2 - x ²

Passo 1

Fala ai, belezinha?

Nesta questão temos queidentificar as curvas, rearranjar a equação em termos de x e y . Desenhar e analisar o gráfico.

Passo 2

Para se desenhar o mapa de contorno, precisa-se chegar à função das curvas de nível.

Basta fazer f x , y = k e depois ir variando k (dando valores) para representar algumas curvas de nível no mapa.

Passo 3

f x , y = y 2 - x 2 = k

ATENÇÃO: Como k   é igual a uma raiz, temos que k ≥ 0 .

y 2 - x 2 = k 2

Essa é a equação de uma hipérbole

y 2 =   x 2 + k 2

y = ± x 2 + k 2

As curvas de nível da função f ( x , y ) = x 2 + k 2 ​ incluem duas linhas retas para c = 0 e hipérboles para c > 0 , todas centradas na origem. Não há curvas de nível para c < 0 , pois a raiz quadrada de um número negativo não é definida no conjunto dos números reais.

Passo 4

Vamos considerar algumas condições para a euqaçãoda hipérbole.

y 2 - x 2 = k 2

Para k = 0 :

y 2 - x 2 = 0

y ± x

Para k > 0 :

y 2 - x 2 = k 2

Este é uma hipérbole com eixos y-centrada.

Para k < 0 :

Não há solução, pois a raiz quadrada de um número negativo não é real.

Passo 5

Variando k , chega-se ao seguinte mapa de contorno:

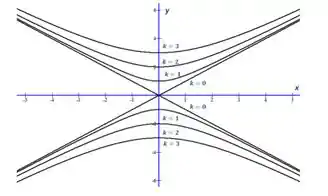
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A, bem como os pontos em que estes valores são atingidos. f x , y = 2 x + y + 3eA = x , y ∈ I R 2x ≥ 0 , y ≥ 0
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A, bem como os pontos em que estes valores são atingidos. f x , y = y x - 1eA = x , y ∈ I R 2 - 1 ≤ x ≤ 0 , 1
Determine, caso existam, os valores máximo e mínimo de f em A; determine, também os ponrots em que esses valores são atingidos f x , y = 2 - x ² + y ²eA = { ( x , y ) ∈ I R 2 ² ² }
Um ponto P descreve uma curva sobre o gráfico da função f ( x ,y )=x²+y² ² ² de modo que a sua projeção Q sobre o plano xy descreve a reta x+y=1 . Determine o ponto da curva que se encontra mais próxi
Raciocinando geometricamente, determine, caso existam, os valores máximo e mínimo de f em A , bem como os pontos em que estes valores são atingidos. f x , y = y x - 1 e A o círculo x - 3 2 + y - 1 2 ≤