Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 25
Utilize coordenadas cilíndricas.
- Ache o volume da região limitada pelo paraboloide e o cone .
- Encontre o centroide do (centro de massa no caso em que a densidade é constante).
Passo 1
Faaaala galera, tudo bem?
Vamos começar!
Precisamos usar coordenadas cilíndricas para resolver o item (a) e (b).
No item (a) precisamos achar o volume da região , que é limitada por um paraboloide e um cone, com suas expressões respectivamente:
Já no item (b), precisamos achar o centroide de (que é o centro de massa, considerando a densidade constante).
Bastante informação né? Vamos com calma pensar juntos, beleza!?
Para o item (a), vamos lembrar da expressão do volume:
Onde,
Do enunciado temos a variação de , que é do cone até o paraboloide:
Como saber quem esta acima? É só você fazer e em cada expressão, e ver qual tem o maior valor de .
Para obter os intervalos em e , temos que igualar as expressões em . Porque isso? Assim vamos obter uma expressão de dependa apenas de e , ficando mais fácil de expressão os intervalos de variação.
Logo vamos perceber que precisamos aplicar uma mudança para coordenadas cilíndricas do tipo:
Você vai cair em uma expressão do segundo grau para o raio, ai é so você fazer baskara e achar as raízes. Nesse caso, você deve considerar apenas o raio positivo.
Feito isso, você terá o intervelo de variação do raio, que vai de até o valor encontrado. Para o ângulo temos:
Para o item (b) precisamos lembra das definiçoies de centroide. Então temos que:
Basta aplicarmos essas equações e encontramos o centroide. Lembre-se que a dendidade é constante.
E que a densidade, massa e volume estão relacionados pela equação:
Sabendo disso, vamos colocar mão na massa!
Bora lá!!!
Passo 2
Vamos começar pelo item (a).
Como quem estará por cima é o paraboloide, temos que varia do cone até o paraboloide:
Substituindo na integral do volume:
Onde,
Então, temos:
Para saber que região é essa, precisamos igualar os ’s:
Fazendo a mudança de coordenadas cilíndricas, onde temos:
Substituindo, temos:
Utilizando a relação trigonométrica:
Vamos ter:
Resolvendo essa equação por baskara, temos que as raízes são:
Mas não temos valores negativos para . Então, a região de integração é dada por coordenadas cilíndricas:
Passo 3
Agora precisamos calcular a integra do volume:
Escrevendo tudo em coordenadas cilíndricas, temos:
Lembre-se, começamos integrando de dentro para fora. Integrando em , temos:
Aplicando os limites de integração, vai ficar:
Integrando em , vamos ter:
Aplicando os limites de integração, ficamos com:
Simplificando, temos:
Integranndo em , vamos ter:
Aplicando os limites de integração, obtemos como resposta:
Passo 4
Agora vamos resolver o item (b).
Sabemos que densidade, massa e volume estão relacionados, certo?
Podemos escrever a massa como:
Sabemos que a densidade é constante, e volume encontramos no item (a).
Logo temos que:
Agora vamos calcular os centroides, mas antes precisamos determinar os momentos:
Aqui vamos dar uma pausa nos cálculos e analisar um pouco nossa região.
Sabemos que nossa região varia do cone até o paraboloide:
Com o auxilio do Geogebra, temos a seguinte região:
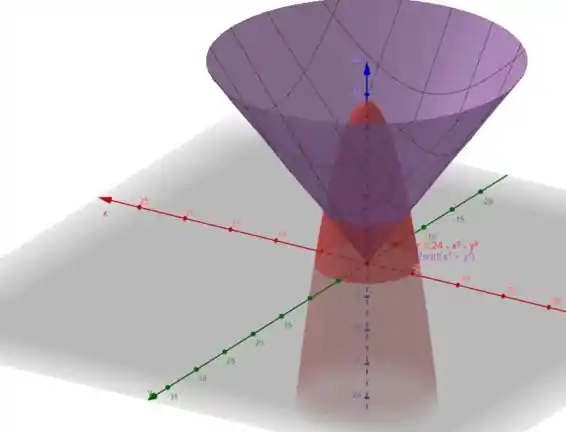
Em roxo temos o cone, e em vermelho o paraboloide.
Observe que em relação ao plano e ao plano temos simetria. E quando isso acontece o momento em relação a esse plano é zero.
Sabendo disso, podemos concluir que:
Logo, nos resta calcular o momento :
Substituindo em cordenadas cilíndricas, temos:
Passo 5
Agora precisamos começar a integrar. Mas lembre-se, que começamos de dentro para fora.
Integrando em , temos:
Aplciando os limites de integração:
Integrando em agora. Vamos ter:
Aplicando os limites, temos:
Por fim, ficamos com umaintegral simples em . Integrando, ficamos com:
Aplicando novamente os limites de integração, temos:
Logo, podemos escrever nossos centroide como:
Como concluímos que e vão ser zeros devido a simetrianos planos e , temos que o centroide é: