1. Utilize coordenadas cilíndricas para mostrar que o volume do sólido limitado por cima pela esfera , e por baixo pelo cone , onde é
2. Deduza que o volume da cunha esférica dada por , e
3. Utilize o teorema do Valor Médio para mostrar que o volume da parte pode ser escrito como

Onde está entre e , está entre e , , e

(a)

Bom, o sólido que a gente quer calcular o volume é limitado por um cone e uma esfera, então é assim:

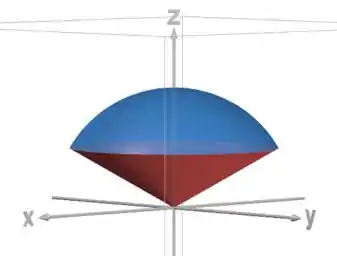
O cone (em vermelho) tem equação:

Onde é um ângulo fixo (constante), entre e .

E a esfera (em azul) é:

Como estamos na parte positiva de ,

Nosso sólido está acima do cone e abaixo da esfera, então:

Para encontrar os limites de , vamos olhar para um corte do sólido no plano (pode ser qualquer corte vertical, que chegamos no mesmo resultado!)

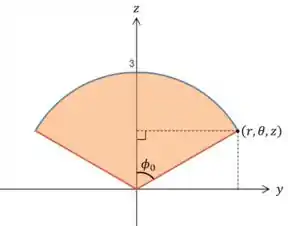
Vamos marcar as distâncias que sabemos nessa imagem.

• Esse ponto marcado faz parte tanto do cone quanto da esfera. Então, a distância dele até a origem é (o raio da esfera)
• Já a altura dele é (equação do cone)
• A distância projetada no plano (nesse caso, no eixo ) do ponto até a origem é

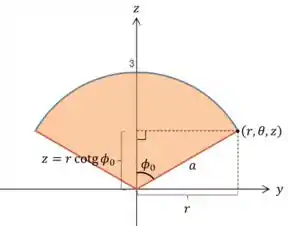
Como esse triângulo que inclui o ângulo é retângulo, podemos calcular o seno de como:

Percebe que essa distância varia desde até esse valor que acabamos de calcular, então:

Já com relação aos limites de , como o nosso sólido envolve todo o eixo , não existe nenhuma limitação para :

Assim, tendo todos os limites das variáveis, podemos escrever a integral que representa o volume desse sólido :

Transformando em coordenadas cilíndricas (lembrando de incluir o jacobiano):

Agora, vamos integrar, de dentro pra fora.

Primeiro, em função de , considerando e como constante:

Podemos tirar dessa primeira integral, por ser constante:

Agora vamos integrar em função de , com constante. Como o integrando não depende de , pode sair todo dessa integral:

Então:

Por último, vamos integrar em função de .

Primeiro, vamos separar em duas integrais:

Essa primeira integral, vamos calcular usando a substituição :

Como ,

Então:

Podemos tirar e das integrais, por serem constantes, e aí conseguimos integrar:

Como a primitiva de é:

Então:

Substituindo nos limites de integração:

Vamos colocar em evidência:

Como :

Colocando em evidência:

Já que :

E provamos a letra (a)!

(b)

De novo, vamos usar de que o volume é a integral de . Sendo a cunha esférica com:

Então:

Pra transformar isso em integral iterada, usamos coordenadas esféricas (os limites das variáveis são dados pela descrição de ). Lembrando de incluir o jacobiano, a integral fica:

Agora vamos calcular essa integral!

Como nossos limites de integração são constantes, e conseguimos separar o integrando em um produto de funções de cada uma das variáveis, podemos separar essa integral em três integrais simples:

E aí podemos calcular cada uma das integrais direto:

Então, o volume fica:

E provamos a fórmula!

(c)

A gente quer transformar essa fórmula que acabamos de achar nisso aqui:

Bom, como , já fazemos essa mudança:

Agora vamos olhar separado pras expressões que envolvem e .

Começando com :

Vamos definir uma função :

De forma que a nossa expressão é exatamente a diferença . Assim, podemos aplicar o TVM: já que essa é uma função contínua e derivável, existe um entre e que:

A derivada de é:

Então:

E por enquanto nossa fórmula está assim:

Agora olhando pro :

Vamos definir uma outra função:

E assim a nossa expressão é a diferença entre .

Pelo TVM, existe um   entre e tal que:

Calculando a derivada de :

Então:

Então o volume fica:

E provamos a fórmula do enunciado!