Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 35
As curvas de nível (isotérmicas) são mostradas para a temperatura da água (em °C) em Long Lake (Minnesota) em 1998 como uma função de profundidade e da época do ano. Estime a temperatura do lago em 9 de junho (dia 160) em uma profundidade de 10 m e em 29 de junho (dia 180) em uma profundidade de 5 m.
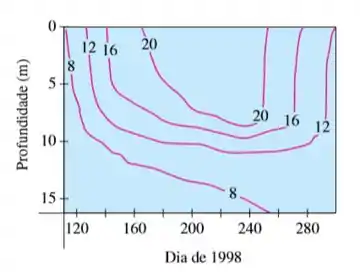
Passo 1
Fala aí! Partiu resolver essa questãozinha juntos!!
A gente tem as curvas isotérmicas para a temperatura da água no gráfico abaixo:
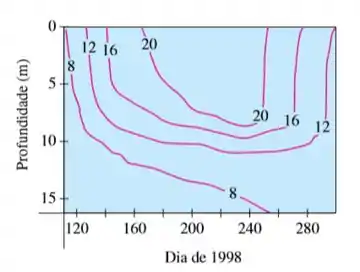
As isotermas são linhas de mesma temperatura, isso significa que caminhando na linha isoterma, teremos a mesma temperatura, mesmo com diferentes profundidades.
Bom, precisamos encontrar a temperatura no dia , a uma profundidade de m e no dia a uma profundidade de m.
Podemos encontrar esses resultados analisando o gráfico que nos foi dado, ok? Vamos ter que gerar uma aproximação, iremos marcar a reta de profundidade e iremos marcar a reta de dia, no encontro dessas duas retas, poderemos interpretar em qual temperatura a água está.
Passo 2
No dia , numa profundidade de metros, vamos estar entre as curvas de e , olha só:
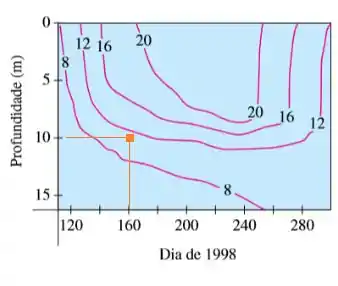
Podemos ver que o ponto está mais próximo da curva de , então podemos estimar uma temperatura em torno de , beleza?
Já no caso do dia , a uma profundidade de 5 m, estamos entre as curvas de e , como mostramos aqui:
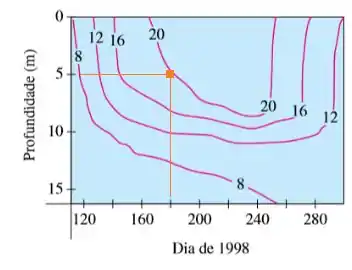
Estamos em um ponto muito próximo da curva de , então podemos estimar que a temperatura, nesse caso, deve ser em torno de .
Show de bola! Conseguimos!
Resposta
No dia 160, numa profundidade de 10 metros, estimamos e no dia 180, numa profundidade de 5 metros, estimamos .