Quando estudam a formação de cordilheiras, os geólogos estimam a quantidade de trabalho necessária para erguer uma montanha a partir do nível do mar. Considere uma montanha que tenha essencialmente o formato de um cone circular reto. Suponha que a densidade do material na vizinhança de um ponto seja e a altura seja
- Determine a integral definida que representa o trabalho total exercido para formar a montanha.
- Assuma que o monte Fuji no Japão tenha o formato de um cone circular reto com raio de , altura e densidade constante de . Quanto trabalho foi feito para formar o monte Fuji se a terra estivesse inicialmente ao nível do mar?
Passo 1
Olá, tudo bem?
Nessa questão, ele explica que os geólogos quando estudam a formação de cordilheiras, estimam a quantidade de trabalho necessária para erguer uma montanha a partir do nível do mar.
Ele pede para considerar uma montanha que tenha essencialmente o formato de um cone circular reto. Suponha que a densidade do material na vizinhança de um ponto seja e a altura seja
Com essas informações deve responder o item (a) e (b). Onde,
(a) Determine a integral definida que representa o trabalho total exercido para formar a montanha.
(b) Assuma que o monte Fuji no Japão tenha o formato de um cone circular reto com raio de , altura e densidade constante de . Quanto trabalho foi feito para formar o monte Fuji se a terra estivesse inicialmente ao nível do mar?
Eu sei que é muita informação que ele nos deu.
Mas calma. Vamos pesar juntos nessa, beleza!?
Para o item (a).
O trabalho total vai ser igual à força gravitacional:
Onde, é a massa total, é a altura e é a gravidade que, ao nível do mar, é .
A gente sabe, que podemos relacionar densidade, massa e volume. Essa relação é descrita como:
Onde, é a densidade, é a massa e é o volume.
Sabendo disso, podemos pensar na seguinte situação. Para elevar um pedacinho:
do monte até um ponto , vamos ter um pedacinho de trabalho:
Se quisermos saber o trabalho total é só integrar ambos os lados. Mas essa eu vou deixar para vocês, senão a resposta vai estar aqui na estratégia né hahahaha
Para o item (b).
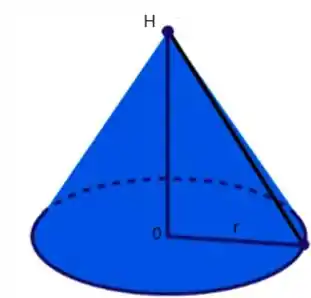
Para essa parte vamos ter que desenhar um recorte desse cone na forma de um triangulo retângulo. Porque ai conseguimos achar uma expressão para o raio em função da altura, que é nosso objetivo.
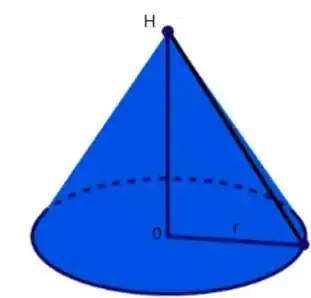
Pois sabemos a variação do ângulo e da altura:
Assim, vamos montar nossa integral e resolve-la. Com a expressão do trabalho encontrada, basta aplicarmos os valores dados no enunciado.
Borá fazer essas etapas juntos!!!
Passo 2
Vamos começar pelo item (a)
Sabemos que o trabalho pode ser escrito como:
Onde, é a massa total, é a altura e é a gravidade que, ao nível do mar, é .
Vamos escrever a massa como um elemento infinitesimal, ou seja, um pedacinho de massa em função do volume e da densidade.
Logo temos:
Onde, é a densidade fornecida no enunciado.
Logo, o trabalho para elevar um pedacinho de massa é:
Substituindo , temos:
Cuidado para não confundir os aqui, um é gravidade e o outro é densidade. Vamos colocar o valor da gravidade, para evitar qualquer confusão. Logo temos:
Para obter a integral, integramos de ambos os lados. Ficamos com:
A integral de , vai ser o próprio .
Assim temos como resposta:
Passo 3
Agora vamos para o item (b).
Digamos agora que a montanha tem a forma de um cone, podemos fazer um desenho da fatia lateral da relação entre a altura total e do raio grande com algum ponto intermediário com altura e raio :
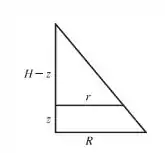
Como é um cone circular reto, podemos fazer a seguinte comparação em triângulo retângulo:
Assim a distância em termos da altura é:
Dado que a densidade é constante de , a altura máxima e raio máximo , o volume vai ser, em coordenadas cilíndricas:
E o diferencial de volume é
Agora é só juntar tudo isso na integral do volume que encontramos no passo anterior.
Assim, temos:
Colocando os intervalos de integração, vamos ficar com:
Passo 4
Agora vamos começar a integrar. Lembre-se, começamos a integrar de dentro para fora.
Vamos integrar primeiro, e só no final substituir os valores de e .
Logo, integrando em :
Aplicando os limites temos:
Simplificando, temos:
Agora vamos fazer a integração em relação à . Logo, temos:
Aplicando os limites de integração, vamos ter:
Simplificando, ficamos com:
Passo 5
Ficamos com uma integral simples em . Integrando, temos:
Aplicando os limites de integração e simplificando, vamos ficar com a seguinte expressão:
Agora é só substituir os valores de e fornecidos no enunciado:
Substituindo, temos:
Logo, nossa resposta é: