Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 25
Utilize uma ferramenta gráfica como no Exemplo 4 (ou o Método de Newton ou um determinador de raízes) para encontrar os pontos críticos de com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico.
Passo 1
Show de bola, galera....Vamos às contas...
Neste exercício, precisamos encontrar e classificar os pontos críticos da função. Vamos calcular as derivadas parciais, resolver o sistema das equações para encontrar os valores de e , em seguida, usar o segundo teste de derivada.
Basicamente precisaremos calcular os seguintes valores:
E aí, meus amigos, não tem mistério!
Depois precisaremos calcular os pontos críticos da função ao fazer .
Na sequência, usaremos o Teste da Derivada Segunda ao calcularmos
e avaliarmos o seu sinal juntamente com o sinal de .
Podem ocorrer três casos:
- então é um mínimo local.
- então é um máximo local.
- então não é nem mínimo e nem máximo local.
Vamos lá?
Passo 2
Calculemos os pontos críticos de da seguinte forma, temos:
E temos sua derivada parcial em relação a :
Temos também:
Precisamos encontrar os zeros dessas duas derivadas:
e
Podemos organizar a segunda equação como:
Isso nos da:
E
Passo 3
Então utilizaremos esses dois resultados para encontrar as raízes em conjunto com o Symbolab, que será nossa calculadora:
Substitindo em :
Temos:
Dividindo por
Usando o GeoGebra:
Agora substituindo
Em:
Utilizando o Symbolab:
Agora a gente colocar essas ultimas raízes que encontramos em:
Então nossos pontos críticos são:
Passo 4
Calculemos o sinal de
Agora vamos encontrar :
Derivando:
Agora iremos encontrar :
E iremos encontrar também :
E por ultimo :
Montando, temos:
Agora iremos analisar o sinal do determinante de e o sinal de para os respectivos pontos críticos:
– Para :
e
Como e , .
Passo 5
– Para :
Como , .
– Para :
E como temos:
Como , .
– Para :
E temos também:
Como e , .
– Para :
A gente tem:
Como e , .
Passo 6
Show de bola, galera. Agora nós iremos apresentar o gráfico da função, só pra ver se o que calculamos está coerente. 
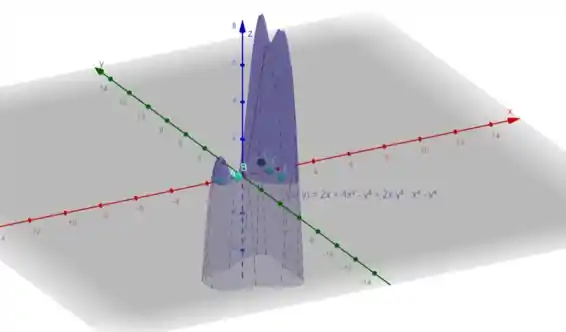
Podemos ver os pontos que encontramos indicados no gráfico gerado no GeoGebra