Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.3 - Ex. 7
Determinando o produto apresentado uma demanda y (em milhares) quando preço, por unidade, é x (em R$). Foram observados os seguintes dados:
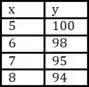
A tabela nos diz que ao preço unitário de 5 reais de demanda foi de 100.000 unidades; ao preço unitário de 6 reais a demanda foi de 98.000 unidades etc.
Passo 1
Vamos usar a questão 5, beleza? Ou seja, resolver aquele sistema, para isso, precisamos encontrar os valores que faltam no sistema abaixo:
Para isso, faremos a seguinte tabela 
Substituindo no sistema,
Após escalonar o sistema, temos que:
Substituindo a equação na função,
Dessa forma, ficamos com:
Resposta
Exercícios de Livros Relacionados
5-20. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vi
5-20. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vi
Mostre que f x , y = x 2 y e - x 2 - y 2 tem valores máximos em ± 1 , 1 2 e valores mínimos em ± 1 ,- 1 2 .Mostre também que f tem infinitos outros pontos críticos e que D = 0 em cada um deles. Quais
Utilize uma ferramenta gráfica para encontrar os pontos críticos de f com precisão de três casas decimais. Em seguida, classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfi
Determine os valores máximos e mínimos locais e pontos de sela da função. f x , y = ( x - y ) ( 1 - x y )