Determine a imagem do conjunto sob a transformação dada.
é o disco dado por ; ,
Passo 1
Fala pessoal, tudo bem? Vamos começar então!!!
Precisamos obter a imagem do conjunto sob a transformação dada:
é o disco dado por:
E,
Vamos com calma aqui, beleza?
Repare que temos a expressão do disco em função de e , e temos também uma relação de e com com os termos e .
Nosso objetivo é escrever uma expressão apenas em função de e , fazendo isso podemos obter a imagem.
Vamos nessa galera!!!
Passo 2
Vamos começar entendo nossa região dada em função de e .
Ele já afirmou que é um disco, certo? E sabemos que um disco nada mais é que um circulo no plano .
Repare na figura:
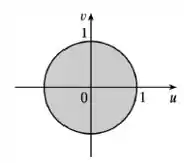
Observe que se trocarmos por e por , vamos ter extamente a expressão do circulo que tanto conhecemos.
Até aqui foi só uma comparação, para compreendermos a região.
Passo 3
Agora vamos isolar e nas equações dadas do disco:
Substituindo, temos:
Observe essa expressão, ela também é muito conhecida. Temos aqui a representação de uma elipse.
Assim, a imagem de é uma região elíptica como na figura abaixo:
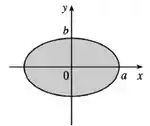
Resposta