Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.9 - Ex. 8
Determine a imagem do conjunto sob a transformação dada.
é o quadrado limitado pelas retas , , ,
Passo 1
E aii, galera!
Nessa questão precisamos achar a imagem de uma transformação!
Basicamente, o que ela quer saber é: se aplicarmos essa transformação a todos os pontos do conjunto , vamos construir um outro conjunto (imagem), que eu vou chamar de . Quem é esse ?
A gente não precisa calcular a transformação em todos os pontos, tá? Basta calcular nos limites do conjunto!
Então vamos começar desenhando esse conjunto (que é uma região de ), e aplicar a transformação nos limites!
Passo 2
Nosso conjunto é um quadrado, vamos dividir o limite em quatro retas:
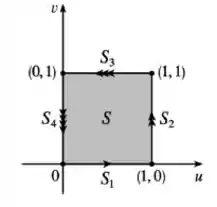
Então primeiro vamos olhar para o lado no plano . é descrito por , e das equações dadas temos:
A imagem dessa reta fica:
E como :
Passo 3
é o segmento de reta , então:
Substituindo na segunda equação:
E como :
Passo 4
é o segmento de reta , então:
Vamos ficar com:
Como :
Passo 5
E por último, é o segmento , então ficamos com:
E ficamos com:
E como :
Passo 6
Resumindo, as imagens das nossas retas são:
Vamos desenhar essas curvas nos intervalos indicados:
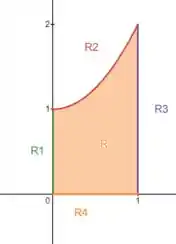
Então, a imagem de é a região entre a curva (que é o ) e o eixo , no intervalo .
Resposta
A região entre a curva e o eixo , no intervalo .