Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.8 - Ex. 07

Utilize a transformacao no Exercicio 3 para calcular a integral

∫ R ∫ 3 x 2 + 14 x y + 8 y 2 d x d y

para a regiao R no primeiro quadrante delimitada pelas retas y = – (3/2)x + 1, y = – (3/2)x + 3, y = – (1/4)x e y = – (1/4)x + 1.

Passo 1

Faaaaalaaa meus abençoados, tudo blz?

Primeiro vamos desenhar o gráfico para a gente entender o funcionamento melhor da questão? Olha só se liga como ficou:

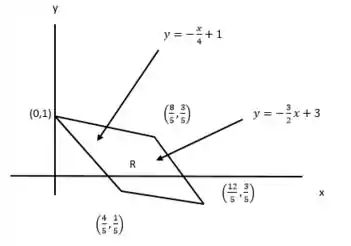
Resolvendo a integral na região R :

∫ R ∫ 3 x 2 + 14 x y + y 2   d x d y = ∫ R ∫ 3 x + 2 y x + 4 y   d x d y

∫ G ∫ u v   ∂ x , y ∂ u , v d u d v = 1 10   ∫ G ∫ u v   d u d v

Passo 2

Aqui para acha os limites de G a partir dos limites de R criei uma tabela para facilitar os entendimentos,

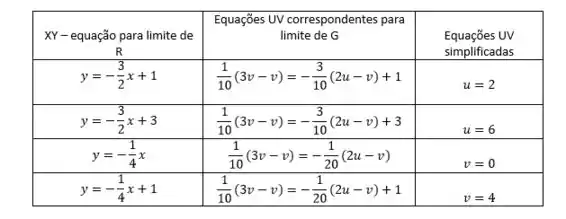
Com isso,

1 10   ∫ G ∫ u v d u d v = 1 10 ∫ 2 6 ∫ 0 4 u v d v d u = 1 10 ∫ 2 6 u   v 2 2 0 4 d u = 4 5 ∫ 2 6 u d u = 4 5   u 2 2 2 6 = 4 5   18 - 2 = 64 2

Resposta

64 2

Exercícios de Livros Relacionados

Calcule o determinante apropriado para mostrar que o jacobiano da transformação do espaço cartesiano rfu para o espaçocartesiano xyz é r2 sen f.
Encontre o jacobiano ∂(x, y, z)/∂(u, v, w) da transformação:a. x = u cos v, y = u sen y, z = wb. x = 2u – 1, y = 3y – 4, z = (1/2)(w – 4)
Volume de um elipsoide Encontre o volume do elipsoide x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 . (Sugestão: sejam x = a u , y = b v e z = c w . Então encontre o volume de uma região apropriada no espaço u v w
Centroide de um semielipsoide sólido Considerando oresultado de que o centroide de um hemisfério sólido estáno eixo de simetria a três oitavos da distância da base aotopo, mostre, transformando as int
Utilize a transformação x = u 2 - v 2 , y = 2 u v para calcular a integral ∫ 0 1   ∫ 0 2 1 - x   x 2 + y 2 d y d x (Sugestão: mostre que a imagem da região triangular G com vértices ( 0,0 ) , ( 1,0 )