Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.7 - Ex. 34
Nos Exercícios 33-38, (a) encontre os limites em coordenadas esféricas para a integral que calcula o volume do sólido dado e em seguida (b) calcule a integral.
O sólido delimitado abaixo pelo hemisfério e acima pela cardioide de revolução
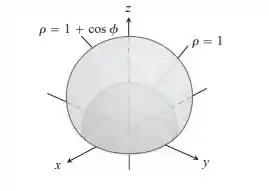
Passo 1
Faaaala, cara! Tranquileba?
Para auxiliar na explicação, temos:
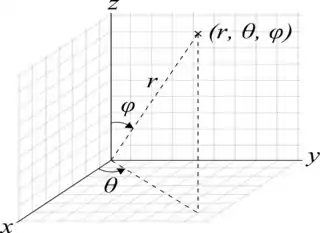
E vendo a imagem vemos que o nosso queridão e nosso amado e tendo já dado que . E tendo o Jacobiano das coordenadas esféricas como , temos a integral:
Passo 2
Passo 3
Vamos resolver cada item separadamente
Para:
Façamos logo e quando e para
Para:
O primeiro:
O segundo:
Das técnicas de integração temos que:
Assim:
Assim:
Para:
Para o primeiro:
Façamos logo e quando e para
Para o segundo:
Façamos logo e quando e para
Assim:
Assim, teremos:
O que já era trivial de ser visto e feito desde o começo (é verdade esse bilhete e não contém ironia)