Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.8 - Ex. 08

Utilize a transformacao e o paralelogramo R no Exercicio 4 para calcular a integral

∬ R 2 x - 4 d x d y

Passo 1

Faaaaalaaa meus abençoados, tudo blz?

Então nessa questão ele pede para a gente usar o paralelogramo e a transformação do exercício 4, e para facilitar nossas contas vamos ver o desenho grafico do paralelogramo com suas devidas transformações:

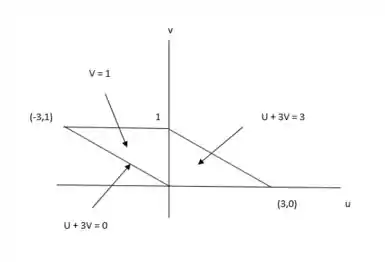
Passo 2

Agora sim resolvendo a integral vamos ter,

∬ R 2 x - 4 d x d y = ∫ G ∫ - 2 v   ∂ x , y ∂ u , v   d u d v =   ∫ G ∫ - 2 v d u d v = ∫ 0 1 ∫ - 3 v 3 - 3 v - 2 v d u d v = ∫ 0 1 - 2 v 3 - 3 v + 3 v d v = ∫ 0 1 - 6 v d v = - 3 v 2 0 1 = - 3

Resposta

-3

Exercícios de Livros Relacionados

Seja D a região no espaço x y z definida pelas desigualdades 1 ≤ x ≤ 2 ,0 ≤ x y ≤ 2 ,0 ≤ z ≤ 1 . Calcule ∭ D   x 2 y + 3 x y z d x d y d z aplicando a transformação u = x ,v = x y ,w = 3 z e integrand
Utilize a transformação x = u / v , y = u v para calcular a soma integral ∫ 1 2   ∫ 1 / y y   x 2 + y 2 d x d y + ∫ 2 4   ∫ y / 4 4 / y   x 2 + y 2 d x d y
Momento de inércia polar de uma placa elíptica Uma placa fina de densidade constante cobre a região delimitada pelaelipse x2/a2 + y2/b2 = 1, a0, b0, no plano xy. Encontre oprimeiro momento da placa em
Calcule uma integral no Exemplo 5 integrando com relação ax, y e z.
Área de uma elipse A área pab da elipse x2/a2 + y2/b2 = 1pode ser encontrada integrando a função ƒ(x, y) = 1 sobre aregião delimitada pela elipse no plano xy. Calcular a integraldiretamente exige uma