Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.4 - Ex. 23

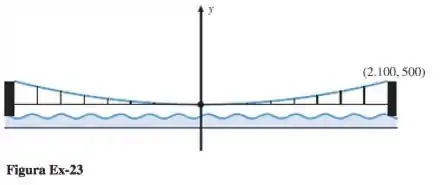
O vão central da ponte Golden Gate (na Califórnia, Estados Unidos) mede 4.200 pés e está suspenso por cabos que sobem 500 pés acima da rodovia em torres de ambos os lados. Aproximadamente, qual é o comprimento da parte do cabo que liga as duas torres dos dois lados? [Sugestão: Como indica a figura abaixo, suponha que o cabo seja modelado por uma parábola y = a x 2 que passa pelo ponto (2.100, 500). Use um CAS ou uma calculadora com capacidade de integração numérica para aproximar o comprimento do cabo. Arredonde sua resposta até o pé mais próximo.]

Passo 1

E aí, tudo joia?

Primeiramente, vamos escrever essa função.

A gente vai considerar uma parábola, da forma y = a x 2 sendo que ela passa pelo ponto ( 2100 ,   500 ) . Podemos fazer isso aqui então ó:

500 = a   2100 2

500 = 4410000   a

a = 500 4410000

a = 0,0001133786

Esse numerozão aí é nosso coeficiente! Nossa função então é:

y = 0,0001133786   x 2

Passo 2

Agora a gente quer o comprimento do arco, sendo que ele vai de x = - 2100 até x = 2100 , certo?

Derivando a função a gente tem:

y ' = 0,0002267573   x

Aí aplicando na fórmula do comprimento:

L = ∫ - 2100 2100 1 + 0,0002267573 x 2   d x

Aí a gente vai jogar isso num Desmos da vida e achar:

L ≈ 4200,00010

Ou seja, o comprimento do cabo é aproximadamente 4200   pés. 😊

Resposta

4200   pés.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva uma integral para o comprimento da curva. Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais. y = y - y
Use a regra de Simpson com n = 10 para estimar o comprimento de arco da curva. Compare a sua resposta com o valor da integral produzido pela sua calculadora. y = xs e nx
Trace a curva estime visualmente seu comprimento. Use sua calculadora para encontrar o comprimento da curva com precisão de quatro casas decimais. y = x 2 + cos ⁡ x ,0 ≤ x ≤ π 2
Use a regra de Simpson com n = 10 para estimar o comprimento de arco da curva. Compare a sua resposta com o valor da integral produzido pela sua calculadora. y = x 3 ,1 ≤ x ≤ 6
Use a regra de Simpson com n = 10 para estimar o comprimento de arco da curva. Compare a sua resposta com o valor da integral produzido pela sua calculadora. y = e - x 2