Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.4 - Ex. 43

Se f (u , v , w) é diferenciável e u = x - y , v = y - z e w = z - x , mostre que

(del f)/(del x) + (del f)/(del y) + (del f)/(del z) = 0

Passo 1

Oi pessoal, com os dados do enunciado, conseguimos fazer os diagramas de árvore, para as três variáveis independentes:

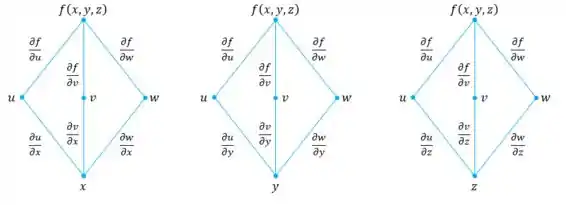
Com isso, através da Regra da Cadeia, temos:

(del f)/(del x) = (del f)/(del u) (del u)/(del x) + (del f)/(del v) (del v)/(del x) + (del f)/(del w) (del w)/(del x)

(del f)/(del y) = (del f)/(del u) (del u)/(del y) + (del f)/(del v) (del v)/(del y) + (del f)/(del w) (del w)/(del y)

(del f)/(del z) = (del f)/(del u) (del u)/(del z) + (del f)/(del v) (del v)/(del z) + (del f)/(del w) (del w)/(del z)

Com os valores dados no enunciado {[[u = x - y],[v = y - z],[w = z - x]]) , conseguimos calcular as derivadas:

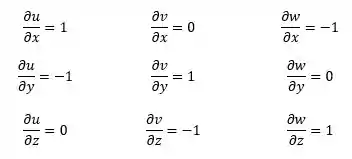
Passo 2

Sendo assim:

(del f)/(del x) + (del f)/(del y) + (del f)/(del z) = (del f)/(del u) (del u)/(del x) + (del f)/(del v) (del v)/(del x) + (del f)/(del w) (del w)/(del x) + (del f)/(del u) (del u)/(del y) + (del f)/(del v) (del v)/(del y) + (del f)/(del w) (del w)/(del y) + (del f)/(del u) (del u)/(del z) + (del f)/(del v) (del v)/(del z) + (del f)/(del w) (del w)/(del z)

= (del f)/(del u) * 1 + (del f)/(del v) * 0 + (del f)/(del w) * (- 1) + (del f)/(del u) * (- 1) + (del f)/(del v) * 1 + (del f)/(del w) * 0 + (del f)/(del u) * 0 + (del f)/(del v) * (- 1) + (del f)/(del w) * 1

= (del f)/(del u) - (del f)/(del w) - (del f)/(del u) + (del f)/(del v) - (del f)/(del v) + (del f)/(del w)

= ((del f)/(del u) - (del f)/(del u)) + ((del f)/(del v) - (del f)/(del v)) + ((del f)/(del w) - (del f)/(del w))

= 0

Logo:

(del f)/(del x) + (del f)/(del y) + (del f)/(del z) = 0

Prontinho pessoal, até mais!

Resposta

Resposta no Passo.

Exercícios de Livros Relacionados

7-12. Use a Regra da Cadeia para achar ∂ z ∂ s e ∂ z ∂ t .9. z = ln ⁡ 3 x + 2 y ,x = s ⋅ s e nt , y = t ⋅ cos ⁡ s
Use a regra da cadeia para achar d z d t z = t g - 1 y x ,x = e t ,y = 1 - e - t
Use a Regra da Cadeia para determinar d z / d t ou d w / d t z = x ln ⁡ x + 2 y , x = s e nt ,y = cos ⁡ t
Use a regra da cadeia para determinar d z / d t ou d w / d t .6- w = x y + y z 2 ,x = e t , y = e ts e nt ,z = e t cos ⁡ t
17-20. Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.19. T = F ( p ,q ,r ) , no qual p = p ( x ,y ,z ) , q = q ( x ,