Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.3 - Ex. 47
A vat with 500 gallons of beer contains 4% alcohol (by volume). Beer with 6% alcohol is pumped into the vat at a rate of 5 galymin and the mixture is pumped out at the same rate. What is the percentage of alcohol after an hour?
Passo 1
A primeira coisa que temos que entender é o que o problema diz. Então temos um tanque com cerveja com de alcool que é tirado dele cerveja a uma taxa de e ao mesmo tempo é reposto neste tanque a mesma taxa de uma outra cerveja com outro teor alcoólico, 6%
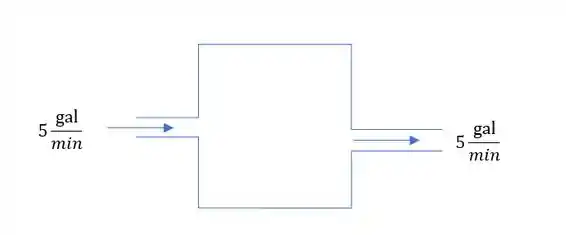
Então temos que escrever essa equação diferencial dessa mistura de álcool
Nós não sabemos como se comporta a mistura de álcool dentro do tanque então deixamos como função de Volume.
Prontinho, agora sim podemos calcular
Passo 2
Agora vamos integrar em ambos os lados
Prontinho. Conseguimos descrever como funciona nosso volume de álcool no tanque. Temos também dados de contorno que nos ajudam a achar C
Logo podemos escrever nossa função como
Para a gente agora descobrir a percentagem de álcool é só dividirmos pelo total de galões e multiplicar por 100.
Onde esse t é medido em minutos. Depois de uma hora teremos
Então terminamos por aqui. Te vejo na próxima resolução
: )