Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.4 - Ex. 65

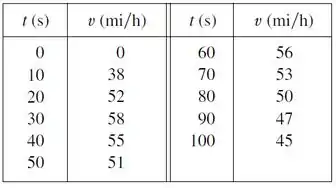
A velocidade de um carro foi lida de seu velocímetro em intervalos de 10 segundos e registrada na tabela. Use a Regra do Ponto Médio para estimar a ditância percorrida pelo carro.

Passo 1

Fala, aí! Vamos resolver essa questão juntos 😊?

A tabela dada apresenta os valores da velocidade v ( t ) de um carro, medida em intervalos de tempo de 10 segundos.

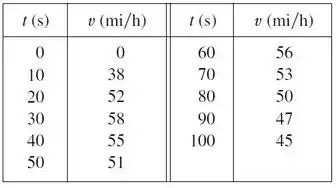
Com essas informações, temos que usar a Regra do Ponto Médio para estimar qual foi a

distância (em milhas) percorrida pelo carro no tempo total de 100 segundos.

A Regra do Ponto Médio diz o seguinte: uma aproximação para uma integral definida em a ,   b é dada por uma soma de Riemann onde os pontos amostrais são os pontos médios de cada subintervalo em que [ a ,   b ] foi dividido.

Matematicamente, temos o seguinte:

∫ a b f t d t ≈   ∑ i = 1 n f t i - Δ t ,

onde n é o número de subintervalos em que [ a ,   b ] foi dividido, Δ t = b - a n é o comprimento dos subintervalos e

t i - = 1 2 t i - 1 + t i

é o ponto médio do intervalo t i - 1 ,   t i .

Pelo visto, se temos que utilizar essa Regra, então vamos ter que calcular uma integral, né?

🤔 Mas qual função temos que integrar?

Bem, conhecemos alguns valores da função velocidade v ( t ) , certo? Além disso, a velocidade é a taxa de variação da posição s ( t ) , né? Ou seja,

v t = s ' t .

Pelo Teorema da Variação Total, vale que a mudança na velocidade do instante t 1 até t 2 é dada por

∫ t 1 t 2 v t d t = s t 2 - s t 1 .

Logo, vamos integrar a função v ( t ) !

🤔 E quais são os limites de integração t 1 e t 2 ?

Como o intervalo total de tempo é 100 segundos, então a integral definida será

∫ 0 100 v t d t =   s 100 - s 0 .

🤔 Mas como fazemos isso se não sabemos a expressão das funções v ( t ) e s t ?

É exatamente por isso que vamos usar uma aproximação da integral por soma de Riemann, conforme dito na Regra do Ponto Médio.

Agora que já temos mais informações, bora resolver essa questão 🤓?

Passo 2

Vamos começar obtendo cada termo da soma de Riemann

∑ i = 1 n v t i - Δ t ,

beleza?

Primeiro, escolhemos dividir o intervalo [ 0 ,   100 ] em n = 5 subintervalos de comprimento

Δ t = 100 - 0 5 = 2 0 .

⚠️Como a velocidade está em milhas/hora e o tempo em segundos, então temos que converter a unidade de Δ t para horas:

1   s e g u n d o = 1 3600 h o r a s .

Dessa forma:

Δ t = 20 3600 = 1 180 .

Além disso:

  • Para o subintervalo [ 0 ,   20 ] temos como ponto médio

    • t 1 - = 1 2 0 + 2 0 = 1 0 .

  • Para o subintervalo [ 2 0 ,   4 0 ] temos como ponto médio

    • t 2 - = 1 2 2 0 + 4 0 = 3 0 .

  • Para o subintervalo [ 4 0 ,   6 0 ] temos como ponto médio

    • t 3 - = 1 2 4 0 + 6 0 = 5 0 .

  • Para o subintervalo [ 6 0 ,   8 0 ] temos como ponto médio

    • t 4 - = 1 2 60 + 80 = 70 .

  • Para o subintervalo [ 8 0 ,   10 0 ] temos como ponto médio

t 5 - = 1 2 80 + 100 = 90 .

Agora, usando a regra do Ponto Médio, temos

∫ 0 100 v ( t ) d t ≈   ∑ i = 1 5 v x i - ⋅ 1 180 ,

ou seja,

∫ 0 100 v t d t ≈ 1 180 ⋅ [ v 1 0 + v 3 0 + v 5 0 + v 70 + v 90 ] .

Vamos calcular o valor aproximado dessa integral no próximo passo 😉!

Passo 3

Vamos dar uma olhada na tabela novamente!

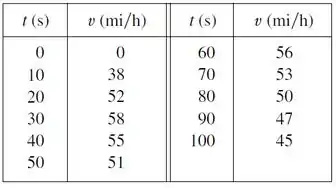
Observe que:

  • No ponto t = 1 0 vale que v 1 0 = 38 .
  • No ponto t = 3 0 vale que v 3 0 = 5 8 .
  • No ponto t = 5 0 vale que v 5 0 = 51 .
  • No ponto t = 7 0 vale que v 7 0 = 53 .
  • No ponto t = 9 0 vale que v 9 0 = 47 .

Dessa forma, como

∫ 0 100 v t d t ≈ 1 180 ⋅ [ v 10 + v 30 + v 50 + v 70 + v 90 ] ,

então

∫ 0 100 v t d t ≈ 1 180 ⋅ 38 + 58 + 51 + 53 + 47 ≈ 247 180 ≈ 1 , 4 .

Assim, uma estimativa para a distância (em milhas) percorrida pelo carro no tempo total de 100 segundos é 1 , 4   m i l h a s .

Resposta

A distância percorrida pelo carro foi de aproximadamente 1 , 4   m i l h a s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calculeint_0^((1)/(2)) ((1)/(sqrt(1 - x^2))) d x
Calculeint_(- 1)^0 e^(- 2 x) d x
Calculeint_((1)/(2))^1 (s + 2) d s
Calculeint_0^((pi)/(3)) (3 + cos 3 x) d x
Calculeint_1^2 ((1 + 3 x^2)/(x)) d x