Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 9
Verificar se o conjunto tem ponto de acumulação.
Passo 1
Galera, seguinte: de uma forma geral, a gente chama de ponto de acumulação qualquer ponto que esteja em uma região de um conjunto infinito de pontos juntinhos. Assim, por exemplo, em um círculo, os pontos todos dele, inclusive a bordinha, são pontos de acumulação, porque eles tem toda essa vizinhança de pontos na mesma região. A chave da questão é essa: vizinhança. Se o ponto for isolado, ele nunca será de acumulação, já que não tem vizinhança!
Passo 2
Vamos marcar os pontos desse conjunto.
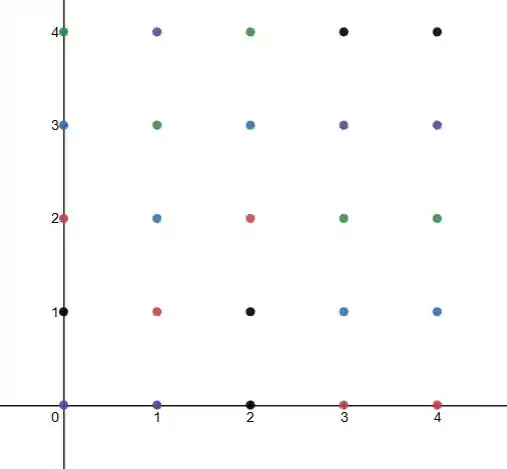
Gente, tem algum ponto aí que não seja isolado? Nenhum! Todos separadinhos. Por isso, esse conjunto não tem ponto de acumulação.
Resposta
Não tem ponto de acumulação.
Exercícios de Livros Relacionados
Identificar as afirmações verdadeiras:d) O conjunto A = { ( x ,y ) | x 2 + 2 x + y 2 - 4 y0 } é conexo.
Identificar quais dos conjuntos seguintes são bolas abertas em R 2 ou R 3 , determinando, em caso positivo, o centro e o raio. x 2 + y 2 + 2 xx - 1 2 + y - 2 2
Identificar quais dos conjuntos seguintes são bolas abertas em R 2 ou R 3 , determinando, em caso positivo, o centro e o raio. x 2 + y 2z 2
Identificar as afirmações verdadeiras:b) A união de bolas abertas é um conjunto aberto.
Verificar quais dos conjuntos a seguir são conexos: A = x ,y ∈ R 2 2 x 2 + 5 y 2 ≤ 10 } B = x , y ∈ R 2 - 1 2 ≤ x ≤ 1 2 C = x , y , z ∈ R 3 3 x 2 + 9 y 2 + z 2 ≥ 18 D = x , y ∈ R 2 y1 x ,x ≠ 0