Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 5

Verificar quais dos conjuntos a seguir são conexos:

Passo 1

Pra gente verificar se um conjunto é conexo, não tem mistério. Funciona assim: desenha o conjunto. Se tiver uma divisão no meio dele que separe o conjunto em duas partes, ele não é conexo. Em qualquer outro caso, é conexo. Vamos amadurecer essa idéia com as questões.

Passo 2

Pra ilustrar bem, vamos começar com o conjunto . Desenhando o gráfico de , podemos ver que a assíntota divide o gráfico em duas partes, e a da esquerda não pode ser conectada com a da direita por um traço sem passar pela parte branca. Por isso, o conjunto não é conexo.

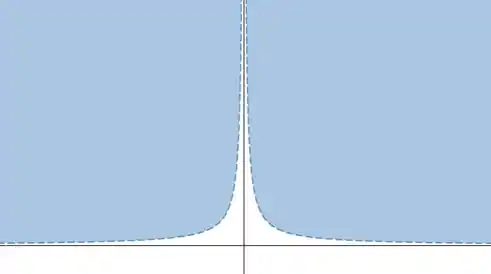
Passo 3

Agora pro conjunto .

Esboçando:

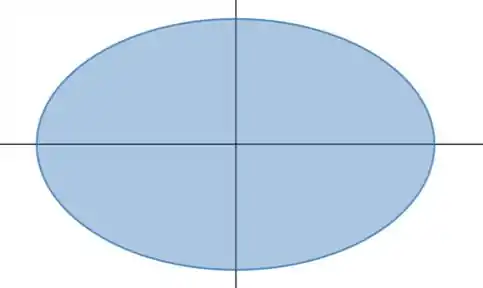
Esse gráfico é de uma elipse, e repara que ela é toda fechadinha, sem nenhuma divisão, e por isso, quaisquer pontos dela podem ser conectados por uma linha. Por isso, o conjunto é conexo.

Passo 4

Agora pro conjunto .

Esboçando,

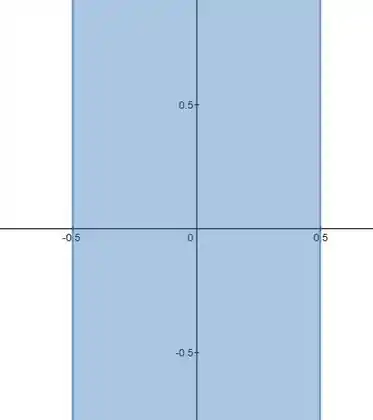
De novo, esse conjunto não tem nada que o divida em duas partes, e então quaisquer pontos do conjunto podem ser ligados sem passar pela parte branca, por isso, ele é conexo.

Passo 5

Agora pro conjunto .

Essa é a equação de um elipsoide, certo? Do mesmo jeito que a gente viu que a elipse era um conjunto conexo, o elipsoide também vai ser, já que também vai ser todo fechadão, igualzinho à elipse, sacou? Então é conexo.