Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.1 - Ex. 3
Considere um triângulo isósceles situado no semipleno e com base paralela ao eixo . Mostre que o volume do sólido obtido pela rotação deste triângulo, em torno do eixo , é igual ao produto da área deste triângulo pelo comprimento da circunferência gerada, na rotação, pelo baricentro do triângulo.
Passo 1
Bem, vamos desenhar esse triângulo:
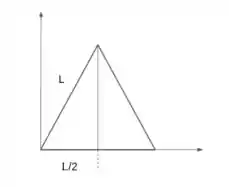
Temos, podemos tirar o tamanho máximo de por Pitágoras:
Portanto, podemos tirar a equação da reta para o triângulo retângulo que a base vai de até .
E para a parte que vai de até
Portanto o volume do sólido é dado por:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x + 1 ,y = 0 , x = 0 , x = 2 ;
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. x = 2 - y 2 , x = y 4 s o b r eoe
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = x 3 , y = 1 ,x = 2 s o b r ey
Encontre o volume do sólido obtido girando a região delimitada pelas curvas dadas sobre a linha especificada. Esboce a região, o sólido e um disco ou arruela típico. y = e x ,y = 0 , x = - 1 , x = 1 s
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x - 1 ,x = 5 ,y = 0