Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.3 - Ex. 4
Calcule o volume do sólido cuja base é um triângulo equilátero de lado e cujas seções perpendiculares a um dos lados são quadrados.
Passo 1
Primeiramente, vamos desenhar esse tal triângulo:
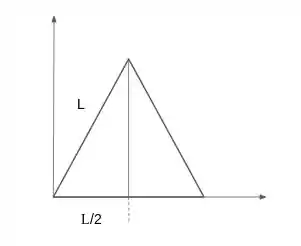
A altura do triângulo é , portanto parametrizando:
Focando somente nessa metade, temos que a área do quadrado formado por fatias desse triângulo é dada por:
Para calcular o volume, precisamos integrar de até :
Como calculamos somente a metade do triângulo, para achar o volume total basta multiplicar por dois, assim:
Resposta
Exercícios de Livros Relacionados
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x ,y = x ;e mt o r n
Use um gráfico para encontrar coordenadas x aproximadas dos pontos de interseção das curvas fornecidas. Em seguida, use sua calculadora para encontrar (aproximadamente) o volume do sólido obtido giran
A integral representa o volume de um sólido. Descreva o sólido. π ⋅ ∫ 1 4 3 2 - 3 - x 2 d x
Use um gráfico para encontrar coordenadas x aproximadas dos pontos de interseção das curvas fornecidas. Em seguida, use sua calculadora para encontrar (aproximadamente) o volume do sólido obtido giran
Determinar o volume do sólido de revolução gerado pela rotação das regiões indicadas, ao redor dos eixos dados. y = x 2 3 e y = 4 ; ao redor dos eixos x = - 9 , y = 0 e x = 0