Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 10

Verifique a aproximação linear dada em a = 0 . A seguir, determine os valores de x   para os quais a aproximação linear tem precisão de 0,1 .

e x cos ⁡ x ≈ 1 + x

Passo 1

E aí! tudo certinho?

Nesse problema temos que verificar a aproximação linear dada por

e x cos ⁡ x ≈ 1 + x

Quando x 0 = a = 0 .

E tambem temos que determinar o intervalo de x onde a aproximação linear tem precisão de 0,1 .

Tem ideia de como fazemos isso?

A aproximação linear de uma função é dada pela reta tangente da função em um ponto

y - y 0 = m x - x 0

Ou seja...

f x ≈ f a + f ' a x - a

Já para determinar o intervalo de x próximo de x = 0 com precisão de 0,1 vamos usar uma ferramenta gráfica para esboçar a reta y = 1 + x e as funções y = e x cos ⁡ x + ∆ x onde ∆ x é a precisão - 0,1 e 0,1 .

Assim, podemos observar o intervalo de x onde a reta pertence a essa precisão.

Bora começar!

Passo 2

Vamos começar verificando a aproximação pela fórmula de linearização:

f x ≈ f a + f ' a x - a

Vamos calcular a derivada pela regra do produto

f ' x = d e x d x · cos ⁡ x + e x · d cos ⁡ x d x

f ' x = e x cos ⁡ x - e x s e n   x

Precisamos calcular f a e f ' a para a = 0 , ou seja

f a = e a cos ⁡ a → f 0 = 1

f ' a = e a cos ⁡ a - e a s e n   a = 1

Substituindo na linearização, temos

f x ≈ f a + f ' a x - a

f x ≈ 1 + 1 x - 0

f x ≈ 1 + x

Então, está verificada!

Tranquilo até aqui?

Passo 3

Para ter uma precisão de 0,1 , precisamos que:

e x cos ⁡ x - 0,1 < 1 + x < e x cos ⁡ x + 0,1

Se ∆ x = - 0,1 , temos

e x cos ⁡ x   - 0,1 < 1 + x

Agora se ∆ x = 0,1

e x cos ⁡ x + 0,1 > 1 + x

Plotando as curvas no plano cartesiano com uma ferramenta gráfica, temos

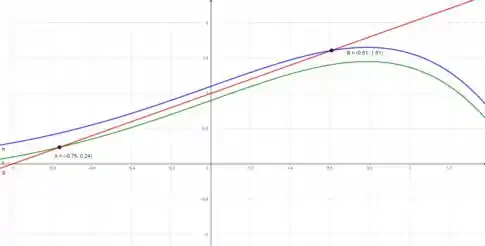
Dessa forma, podemos perceber que para que a precisão seja satisfeita nas proximidades de x = 0 , x deve estar contido no intervalo

- 0,76 < x < 0,61

E aí! o que achou? Responde Aí!

Resposta

- 0,76 < x < 0,61

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a linearização L ( x ) da função em a .f (x) = root(3)(x) , a = - 8
No exemplo 1, o peru é removido do forno quando sua temperatura atinge 185° F e colocado sobre uma mesa em uma sala onde a temperatura é de 75° F. Após dez minutos a temperatura é de 172° F, e após 20
O gráfico indica como a população da Austrália está envelhecendo, apontando o passado e a porcentagem projetada da população com idade superior ou igual a 65 anos. Use uma aproximação linear para prev
Verifique a aproximação linear dada em a = 0 . Então determine os valores de x para os quais a aproximação linear é precisa dentro de 0,1. 1 - x 3 ≈ 1 - 1 3 x
Use o método de Newton com a aproximação inicial especificada x 1 para encontrar x 3 , a terceira aproximação para a raiz da equação dada. (Responda com quatro casas decimais). 2 x 3 - 3 x 2 + 2 = 0 ;