Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 4.1 - Ex. 45

  1. Verifique que y 1 = x 3   e   y 2 = x 3 são linearmente independentes da equação diferencial x 2 y ' ' - 4 x y ' + 6 y = 0 em - ∞ ,   ∞ .
  2. Mostre que W y 1 ,   y 2 = 0 para todo número real.
  3. O resultado da parte (b) viola o Teorema 4.4?
  4. Verifique que Y 1 = x 3 e   Y 2 = x 2 são também soluções linearmente independentes para a equação diferencial no intervalo - ∞ ,   ∞ .
  5. Encontre uma solução para a equação que satisfaça y 0 = 0 ,   y ' 0 = 0
  6. Pelo princípio de superposição ambas as combinações lineares

y = c 1 y 1 + c 2 y 2   e   y = c 1 Y 1 + c 2 Y 2

São soluções para a equação diferencial. Qual delas é a solução geral para a equação diferencial em - ∞ ,   ∞ ?

Passo 1

E aí, tudo bem?

Vish... essa é grande hein?!

Mas calma, vamos por partes que vai sair...

  1. Para mostrar que elas são LI, vamos dar uma olhada nos seus gráficos:

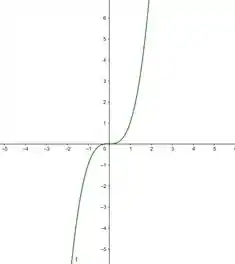
    2. Vemos que as funções não são múltiplas, então elas são linearmente independentes.

    Passo 2

    Agora vamos verificar que elas resolvem a equação x 2 y ' ' - 4 x y ' + 6 y = 0 .

    Para a função y 1 = x 3 , temos:

    y 1 ' = 3 x 2

    y 1 ' ' = 6 x

    Substituindo na EDO, temos:

    x 2 6 x - 4 x 3 x 2 + 6 x 3 = 0

    6 x 3 - 12 x 3 + 6 x 3 = 0

    0 = 0

    E para y 2 = x 3 , para x ≥ 0 é igual a de cima e para x < 0 , temos:

    y 2 ' = - 3 x 2

    y 2 ' ' = - 6 x

    Substituindo:

    x 2 y ' ' - 4 x y ' + 6 y = 0

    x 2 - 6 x - 4 x - 3 x 2 + 6 - x 3 = 0

    - 6 x 3 + 12 x 3 - 6 x 3 = 0

    0 = 0

    Passo 3

  2. Agora vamos verificar que: W y 1 ,   y 2 = 0

    3. Para x ≥ 0 , temos:

    W = x 3 x 3 3 x 2 3 x 2 = 0

    E para x > 0 :

    W = x 3 - x 3 3 x 2 - 3 x 2 = 0

    Então W y 1 ,   y 2 = 0 para qualquer número real.

    Passo 4

  3. Não viola, pois a 2 x = x 2 (que é o termo que acompanha o y ' ' ) é zero quando x = 0 , o que não satisfaz o teorema.

  4. Agora vamos testar se Y 1 = x 3 e   Y 2 = x 2 são soluções linearmente independentes da EDO.

    5. Y ' 1 = 3 x 2

    Y 1 ' ' = 6 x

    Substituindo na EDO:

    x 2 y ' ' - 4 x y ' + 6 y = 0

    x 2 6 x - 4 x 3 x 2 + 6 x 3 = 0

    0 = 0

    E Y 2 = x 2 :

    Y 2 ' = 2 x

    Y 2 ' ' = 2

    Substituindo:

    x 2 2 - 4 x 2 x + 6 x 2 = 0

    2 x 2 - 8 x 2 + 6 x 2 = 0

    0 = 0

    Então também é solução!

    Agora vamos verificar que são linearmente independentes...

    W = x 3 x 2 3 x 2 2 x = 2 x 4 - 3 x 4 = - x 4 ≠ 0

    Então vemos que elas são soluções linearmente independentes.

    Passo 5

  5. Uma solução das que a gente testou aí em cima que satisfaz as condições y 0 = 0   e   y ' 0 = 0 é y = x 3 por exemplo!

  6. Nenhuma é a solução geral, uma vez que formamos a solução geral num intervalo com a x ≠ 0 para todo x no intervalo.

Resposta

  1. Verificação.
  2. Demonstração.
  3. Não
  4. Verificação.
  5. y = x 3
  6. Nenhuma.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 33-40, verifique que as funções dadas formam um conjunto fundamental de soluções para a equação diferencial no intervalo indicado. Forme a solução geral. y ( 4 ) + y ' ' = 0 ;1 , x ,cos
Nos problemas 41-44, verifique que a dada família a dois parâmetros de funções é a solução geral para a equação diferencial não homogênea no intervalo indicado. y ' ' + y = s e cx y = c 1 cos ⁡ x + c
Nos problemas 41-44, verifique que a dada família a dois parâmetros de funções é a solução geral para a equação diferencial não homogênea no intervalo indicado. y ' ' - 7 y ' + 10 y = 24 e x y = c 1 e
Nos problemas 41-44, verifique que a dada família a dois parâmetros de funções é a solução geral para a equação diferencial não homogênea no intervalo indicado. y ' ' - 4 y ' + 4 y = 2 e 2 x + 4 x - 1
Nos problemas 41-44, verifique que a dada família a dois parâmetros de funções é a solução geral para a equação diferencial não homogênea no intervalo indicado. 2 x 2 y ' ' + 5 x y ' + y = x 2 - x y =