Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 09a
O vetor posição de uma partícula em movimento é
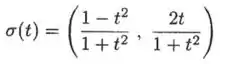
- Mostre que a partícula se move sobre uma circunferência de centro na origem.
Passo 1
A equação de uma circunferência de centro na origem e raio 1 pode ser dada por
Portanto, se nossa função atender esse requisito, é porque de fato se move sobre uma circunferência de centro na origem.
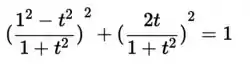
Desenvolvendo, observa-se que a igualdade é satisfeita.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Para resolver os exercícios 16 e 17 , o aluno deve ter familiaridade com as equações diferenciais lineares de segunda ordem com coeficientes constantes.Uma partícula partindo do ponto 1 3 , 0 se move
Um objeto inicia seu movimento no ponto 0 , - 4 , e se move ao longo da parábola y = x 2 - 4 , com velocidade horizontal d x d t = 2 t - 1 . Encontre o vetor posição do objeto, os vetores velocidade e
Considere uma partícula se movendo no plano ao longo da curva definida por: σ t = t - sen t ,1 - cos t , 0 ≤ t ≤ 2 π Determine a velocidade máxima da partícula e o instante em que ela ocorre
Um besouro parte do centro de um relógio muito grande, ao meio-dia, e percorre o ponteiro dos minutos a uma velocidade de 1 c m / s . Suponha que a origem das coordenadas está no centro do relógio. Dê
Dois carros se movem sobre pistas circulares de raios 1k m e 2 k m , respectivamente. O primeiro com velocidade angular constante de 20r d / h . O segundo, parte do repouso, e mantém aceleração angula