Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.4 - Ex. 11

Dois carros se movem sobre pistas circulares de raios 1   k m e 2 k m , respectivamente. O primeiro com velocidade angular constante de 20   r d / h . O segundo, parte do repouso, e mantém aceleração angular constante de 40   r d / h 2 . Suponha que no instante inicial os dois carros estão emparelhados.

  1. Encontre os vetores posição para os dois movimentos
  2. Quanto tempo leva o segundo carro para se emparelhar novamente com o primeiro?
  3. Ache a velocidade do segundo carro neste instante

Passo 1

Beleza, pra começar, vamos lembrar o seguinte galera. Uma circunferência pode ser parametrizada em relação ao parâmetro θ da seguinte forma, sendo R seu raio:

x θ = R cos ⁡ θ

y θ = R sen ⁡ θ

σ θ = R cos ⁡ θ , R sen ⁡ θ

Nessa generalização aí, estamos considerando que a circunferência tem centro na origem, belê? Falando do primeiro carro, temos raio de 1   k m e velocidade angular constante 20   r d / h . Oras, isso quer dizer basicamente que:

d θ d t = 20

E logo:

θ = 20 t + C 1

Vamos ter então pro carro 1, o seguinte vetor posição:

σ 1 t = cos ⁡ 20 t + C 1 , sen ⁡ 20 t + C 1

Isso porque o enunciado não nos dá informação o suficiente pra achar C 1 , o que não é bem um problema. Agora, pro segundo carro, temos raio de 2   k m   e aceleração angular constante 400   r d / h :

d 2 θ d t 2 = 40

d θ d t = 40 t + C 2

Como o segundo carro parte do repouso vamos ter que no instante inicial t = 0 , a velocidade angular d θ d t é nula também! Logo C 2 = 0 . E portanto:

d θ d t = 40 t

θ = 20 t 2 + C 3

E o vetor posição será:

σ 2 t = 2 cos ⁡ 20 t 2 + C 3 , 2 sen ⁡ 20 t 2 + C 3

De novo, não temos como dizer quem é C 3 .

Paciência né hahaha. Mas olha isso, no instante inicial t = 0 temos:

σ 1 0 = cos ⁡ C 1 , sen ⁡ C 1

σ 2 0 = 2 cos ⁡ C 3 , 2 sen ⁡ C 3

E saca só, como os carros estão emparelhados nesse instante, quem quer que seja C 1 , C 3 , vamos ter uma situação como essa:

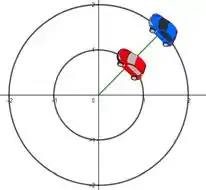
Isso quer dizer que os ângulos são iguais nesse instante! Sendo assim:

C 1 = C 3 = θ o

E o vetor posição dos carros será:

σ 1 t = cos ⁡ 20 t + θ o , sen ⁡ 20 t + θ o σ 2 t = 2 cos ⁡ 20 t 2 + θ o , 2 sen ⁡ 20 t 2 + θ o

Passo 2

Pra gente saber quando os carros vão se emparelhar de novo, basta a gente igualar os ângulos e ver em que instante de tempo isso se repete! Sendo:

σ 1 t = cos ⁡ 20 t + θ o , sen ⁡ 20 t + θ o σ 2 t = 2 cos ⁡ 20 t 2 + θ o , 2 sen ⁡ 20 t 2 + θ o

Teremos:

20 t + θ o = 20 t 2 + θ o

20 t = 20 t 2

t = t 2

O único valor de t que satisfaz essa igualdade sem ser o instante inicial é:

t = 1 h

Passo 3

Pra achar a velocidade do carro, basta a gente derivar o vetor posição. Sendo assim:

σ 2 t = 2 cos ⁡ 20 t 2 + θ o , 2 sen ⁡ 20 t 2 + θ o

V 2 t = σ 2 ' t = - 80 t sen ⁡ 20 t 2 + θ o , 80 t cos ⁡ 20 t 2 + θ o

V 2 1 = - 80 sen ⁡ 20 + θ o , 80 cos ⁡ 20 + θ o

Já a velocidade angular nesse instante a gente pode achar fazendo:

θ t = 20 t 2 + θ o

V θ t = d θ t d t = 8 0 t

V θ 1 = 8 0   r a d / h

Resposta

  1. σ 1 t = cos ⁡ 20 t + θ o , sen ⁡ 20 t + θ o σ 2 t = 2 cos ⁡ 20 t 2 + θ o , 2 sen ⁡ 20 t 2 + θ o θ o   n ã o   p o d e   s e r   d e t e r m i n a d o   c o m   o s   d a d o s   d o   e n u n c i a d o
  2. Em 1h
  3. P a r a   t = 1 h   t e m o s : V e t o r   v e l o c i d a d e →   - 80 sen ⁡ 20 + θ o , 80 cos ⁡ 20 + θ o V e l o c i d a d e   a n g u l a r →   8 0   r a d / h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule d F → d t e d 2 F → d t 2 . F → t = sen ⁡ 5 ti → + cos ⁡ 4 t j → - e - 2 tk →
Suponha v → t ≠ 0 para todo t . Faça T → t = v → t v t onde v t = v → t . Prove que a → = v d T → d t + d v d tT →
Suponha u → ρ θ = cos ⁡ θ i → + sen ⁡ θ j → , u → θ θ = - sen ⁡ θ i → + cos ⁡ θ j → e r → t = ρ tu → ρ θ ( t ) , com θ = θ t e ρ = ρ t deriváveis até a 2ª ordem num intervalo I . Notação: ρ ˙ = d ρ d
Determine a equação da reta tangente à trajetória da função dada, no ponto dado. F t = 1 t , 1 t , t 2eF 2
Suponha u → ρ θ = cos ⁡ θ i → + sen ⁡ θ j → , u → θ θ = - sen ⁡ θ i → + cos ⁡ θ j → e r → t = ρ tu → ρ θ ( t ) , com θ = θ t e ρ = ρ t deriváveis até a 2ª ordem num intervalo I . Notação: ρ ˙ = d ρ d