Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 6
Você planeja fechar um canto do primeito quadrante com um segmento de reta de unidades de comprimento, que vai de a . Demonstre que a área do triângulo determinado pelo segmento e máximo quando
Passo 1
A nossa situação é a seguinte:
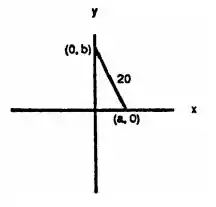
A área vai ser
Além disso, usando Pitágoras, vamos ter:
Isolando o
Como está no primeito quadrante, vamos pegar a parte positiva
E a área vai ficar:
Onde o valor máximo que pode assumir é , quando a barra estiver toda na vertical e o mínimo é , quando a barra estiver toda na horizontal.
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Vamos derivar usando a regra do produto:
Colocando a raiz como potência:
Não podemos esquecer a regra da cadeia durante a derivação:
Fazendo isso igual a
Multiplicando cruzado:
Pelo intervalo, temos:
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
O maior dos valores é quando
Entao o retângulo tem dimensões:
Logo
Resposta
Ei, a resposta está no passo a passo :)